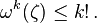Wirtinger inequality (2-forms)

For other inequalities named after Wirtinger, see Wirtinger's inequality.

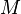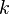In mathematics, the Wirtinger inequality for 2-forms, named after Wilhelm Wirtinger, states that on a Kähler manifold , the of the symplectic form (Kähler form) ω, when evaluated on a simple (decomposable) 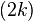-vector ζ of unit volume, is bounded above by 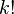. That is,

In other words, 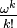is a calibration on 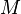. An important corollary is that every complex submanifold of a Kähler manifold is volume minimizing in its homology class.

See also

• 2-form
• Gromov's inequality for complex projective space
• Systolic geometry

References

• Victor Bangert; Mikhail Katz; Steve Shnider; Shmuel Weinberger: E_7, Wirtinger inequalities, Cayley 4-form, and homotopy. Duke Math. J. 146 ('09), no. 1, 35-70. See arXiv:math.DG/0608006