Turán's brick factory problem

Unsolved problem in mathematics:

Is there a drawing of any complete bipartite graph with fewer crossings than the number given by Zarankiewicz?
(more unsolved problems in mathematics)

An optimal drawing of

K 4,7

, with 18 crossings

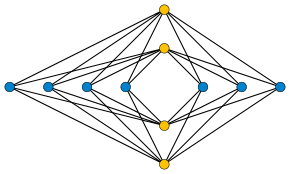
In the mathematics of graph drawing, Turán's brick factory problem asks for the minimum number of crossings in a drawing of the complete bipartite graph $K m,n$ .^[1] More precisely, the graph should be drawn in the plane with each vertex as a point, each edge as a curve connecting its two endpoints, and no vertex placed on an edge that it is not incident to. A crossing is counted whenever two edges that are disjoint in the graph have a nonempty intersection in the plane.

During World War II, Hungarian mathematician Pál Turán was forced to work in a brick factory, pushing wagon loads of bricks from kilns to storage sites. The factory had tracks from each kiln to each storage site, and the wagons were harder to push at the points where tracks crossed each other, from which Turán was led to ask his brick factory problem: what is the minimum possible number of crossings in a drawing of a complete bipartite graph?^[2]^[3]

An upper bound established by Kazimierz Zarankiewicz has been conjectured to give the correct answer for every complete bipartite graph, and the statement that this is true has come to be known as the Zarankiewicz crossing number conjecture. The conjecture remains open, with only some special cases solved.

Upper bound

Both Zarankiewicz and Kazimierz Urbanik saw Turán speak about the brick factory problem in different talks in Poland in 1952,^[3] and independently published attempted solutions of the problem, with equivalent formulas for the number of crossings.^[4]^[5] As both of them showed, it is always possible to draw the complete bipartite graph $K m,n$ with a number of crossings equal to

{\textrm {cr}}(K_{m,n})\leq \left\lfloor {\frac {n}{2}}\right\rfloor \left\lfloor {\frac {n-1}{2}}\right\rfloor \left\lfloor {\frac {m}{2}}\right\rfloor \left\lfloor {\frac {m-1}{2}}\right\rfloor

The construction is simple: place $m$ vertices on the $x$ -axis of the plane, avoiding the origin and subdividing the points as evenly as possible between positive and negative $x$ -coordinates. Similarly, place $n$ vertices on the $y$ -axis of the plane, avoiding the origin and subdividing the points as evenly as possible between positive and negative $y$ -coordinates. Then, connect every point on the $x$ -axis by a straight line segment to every point on the $y$ -axis.

However, their proofs that this formula is optimal, that is, that there can be no drawings with fewer crossings, were erroneous. The gap was not discovered until eleven years after publication, nearly simultaneously by Gerhard Ringel and Paul Kainen.^[6] Nevertheless, it is conjectured that Zarankiewicz's and Urbanik's formula is optimal. This has come to be known as the Zarankiewicz crossing number conjecture. Although some special cases of it are known to be true, the general case remains open.

Lower bounds

The Zarankiewicz conjecture is known to be true for the complete bipartite graphs $K m,n$ with $m \leq 6$ .^[7] Although lower bounds are known that apply more generally, they do not match the upper bound for larger values of $m$ .^[8] For each fixed choice of $m$ , the truth of the conjecture for all $K m,n$ can be verified by testing only a finite number of choices of $n$ .^[9]

The conjecture is also known to be true for $K 7,7$ , $K 7,8$ , and $K 7,9$ .^[10] If a counterexample exists, that is, a graph $K m,n$ requiring fewer crossings than the Zarankiewicz bound, then in the smallest counterexample both $m$ and $n$ must be odd.^[7]

Rectilinear crossing numbers

If edges are required to be drawn as straight line segments, rather than arbitrary curves, then some graphs need more crossings. However, the upper bound established by Zarankiewicz for the crossing numbers of complete bipartite graphs can be achieved using only straight edges. Therefore, if the Zarankiewicz conjecture is correct, then the complete bipartite graphs have rectilinear crossing numbers equal to their crossing numbers.^[11]

References

↑ Turán, P. (1977), "A note of welcome", Journal of Graph Theory, 1: 7–9, doi:10.1002/jgt.3190010105 .
↑ Pach, János; Sharir, Micha (2009), "5.1 Crossings—the Brick Factory Problem", Combinatorial Geometry and Its Algorithmic Applications: The Alcalá Lectures, Mathematical Surveys and Monographs, 152, American Mathematical Society, pp. 126–127 .
1 2 Beineke, Lowell; Wilson, Robin (2010), "The early history of the brick factory problem", The Mathematical Intelligencer, 32 (2): 41–48, doi:10.1007/s00283-009-9120-4, MR 2657999 .
↑ Zarankiewicz, K. (1954), "On a problem of P. Turan concerning graphs", Fundamenta Mathematicae, 41: 137–145, MR 0063641 .
↑ Urbaník, K. (1955), "Solution du problème posé par P. Turán", Colloq. Math., 3: 200–201 . As cited by Székely, László A. (2001), "Zarankiewicz crossing number conjecture", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
↑ Guy, Richard K. (1969), "The decline and fall of Zarankiewicz's theorem", Proof Techniques in Graph Theory (Proc. Second Ann Arbor Graph Theory Conf., Ann Arbor, Mich., 1968), Academic Press, New York, pp. 63–69, MR 0253931 .
1 2 Kleitman, Daniel J. (1970), "The crossing number of $K 5, n$ ", Journal of Combinatorial Theory, 9: 315–323, doi:10.1016/s0021-9800(70)80087-4, MR 0280403 .
↑ de Klerk, E.; Maharry, J.; Pasechnik, D. V.; Richter, R. B.; Salazar, G. (2006), "Improved bounds for the crossing numbers of $K m,n$ and $K n$ ", SIAM Journal on Discrete Mathematics, 20 (1): 189–202, doi:10.1137/S0895480104442741, MR 2257255 .
↑ Christian, Robin; Richter, R. Bruce; Salazar, Gelasio (2013), "Zarankiewicz's conjecture is finite for each fixed $m$ ", Journal of Combinatorial Theory, Series B, 103 (2): 237–247, doi:10.1016/j.jctb.2012.11.001, MR 3018068 .
↑ Woodall, D. R. (1993), "Cyclic-order graphs and Zarankiewicz's crossing-number conjecture", Journal of Graph Theory, 17 (6): 657–671, doi:10.1002/jgt.3190170602, MR 1244681 .
↑ Kainen, Paul C. (1968), "On a problem of P. Erdős", J. Combinatorial Theory, 5: 374–377, doi:10.1016/s0021-9800(68)80013-4, MR 0231744

External links

Weisstein, Eric W. "Zarankiewicz's Conjecture". MathWorld.

This article is issued from Wikipedia - version of the 8/7/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.