Sum-free set
In additive combinatorics and number theory, a subset A of an abelian group G is said to be sum-free if the sumset A⊕A is disjoint from A. In other words, A is sum-free if the equation 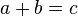 has no solution with
has no solution with 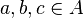 .
.
For example, the set of odd numbers is a sum-free subset of the integers, and the set {N/2+1, ..., N} forms a large sum-free subset of the set {1,...,N} (N even). Fermat's Last Theorem is the statement that the set of all nonzero nth powers is a sum-free subset of the integers for n > 2.
Some basic questions that have been asked about sum-free sets are:
- How many sum-free subsets of {1, ..., N} are there, for an integer N? Ben Green has shown[1] that the answer is
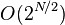 , as predicted by the Cameron–Erdős conjecture[2] (see Sloane's
, as predicted by the Cameron–Erdős conjecture[2] (see Sloane's  A007865).
A007865). - How many sum-free sets does an abelian group G contain?[3]
- What is the size of the largest sum-free set that an abelian group G contains?[3]
A sum-free set is said to be maximal if it is not a proper subset of another sum-free set.
References
- ↑ Ben Green, The Cameron–Erdős conjecture, Bulletin of the London Mathematical Society 36 (2004) pp.769-778
- ↑ P.J. Cameron and P. Erdős, On the number of sets of integers with various properties, Number theory (Banff, 1988), de Gruyter, Berlin 1990, pp.61-79
- 1 2 Ben Green and Imre Ruzsa, Sum-free sets in abelian groups, 2005.
This article is issued from Wikipedia - version of the 3/17/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.