Sigma-ideal

In mathematics, particularly measure theory, a σ-ideal of a sigma-algebra (σ, read "sigma," means countable in this context) is a subset with certain desirable closure properties. It is a special type of ideal. Its most frequent application is perhaps in probability theory.

Let (X,Σ) be a measurable space (meaning Σ is a σ-algebra of subsets of X). A subset N of Σ is a σ-ideal if the following properties are satisfied:

(i) Ø ∈ N;

(ii) When A ∈ N and B ∈ Σ , B ⊆ A ⇒ B ∈ N;

(iii)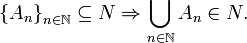

Briefly, a sigma-ideal must contain the empty set and contain subsets and countable unions of its elements. The concept of σ-ideal is dual to that of a countably complete (σ-) filter.

If a measure μ is given on (X,Σ), the set of μ-negligible sets (S ∈ Σ such that μ(S) = 0) is a σ-ideal.

The notion can be generalized to preorders (P,≤,0) with a bottom element 0 as follows: I is a σ-ideal of P just when

(i') 0 ∈ I,

(ii') x ≤ y & y ∈ I ⇒ x ∈ I, and

(iii') given a family x_n ∈ I (n ∈ N), there is y ∈ I such that x_n ≤ y for each n

Thus I contains the bottom element, is downward closed, and is closed under countable suprema (which must exist). It is natural in this context to ask that P itself have countable suprema.

A σ-ideal of a set X is a σ-ideal of the power set of X. That is, when no σ-algebra is specified, then one simply takes the full power set of the underlying set. For example, the meager subsets of a topological space are those in the σ-ideal generated by the collection of closed subsets with empty interior.

References

• Bauer, Heinz (2001): Measure and Integration Theory. Walter de Gruyter GmbH & Co. KG, 10785 Berlin, Germany.