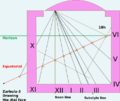
Schema for vertical declining dials

A dial constructed using Waugh's schema

Vertical declining dials are sundials that indicate local apparent time. Vertical south dials are a special case: as are vertical north, vertical east and vertical west dials. The word declining means that the wall is offset from one of these 4 cardinal points. There are dials that are not vertical, and these are called reclining dials.^[1]

A sundial schema uses a compass and a straight edge to firstly to derive the essential angles for that latitude, then to use this to draw the hourlines on the dial plate. In modern terminology this would mean that graphical techniques were used to derive and and from it . ^{[lower-alpha 1]}

Basic calculation

There are four basic angles that are needed to construct a vertical declining dial, Waugh described them such: ^[2]

• SD- Sub-style distance - this is the angle on the dial plate between the foot of the style and the vertical noon line.
• SH- Sub-style height - this defines the slope of the style. It has no effect on the design of the dial plate.
• DL- Difference in longitude- in drawing the dial, DL represents the hour/angle (polar angle)Holwell, John (1712). Clavis Horologiae.  ^{[lower-alpha 2]} when the shadow passes under the style.
• AV- Angle to vertical? -this is used to fix a starting point, in the final stage of laying out equal hours with a protractor. With a calculator this can be easily be derived from the SD and DL, when using compass and ruler it is a construction base line. It never appears on the final dial.

The four basic calculation have a certain symmetry.

• tan (SD) = sin (D). cot(φ)
• sin (SH) = cos (D). cos(φ)
• cot (DL) = cot (D). sin(φ)
• cot (AV) = sin (D). tan(φ)

Waugh's method 1973

• A semicircle is drawn, with a descending vertical.
• For a morning dial, or south-east decliner, a right angles triangle is drawn to the left with a top angle being the co-latitude.
• A second triangle is drawn to the right, with a top angle of D, the declination of the wall.

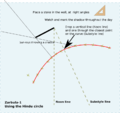
Finding SD- the substyle length

• The bottom bar of the left triangle represents cot Φ. The length is noted and using dividers copied over to the right triangle hypotenuse, and a further horizontal bar drawn. that will have the length of sin D. This is measured and placed on the bottom bar of the left triangle. This sets the position M, and the substyle line (the term diallist use for the angle).

Finding SH - the substyle height

• The height of the right triangle is noted, and a line of this length is swung from point M, till it touches the circle. The angle from the origin to here, is the substyle height.(the term diallist use for the angle).^{[lower-alpha 3]}

Drawing the hourlines

At this point only three lines matter, the vertical, the substyle length and substyle height. A circle marked off in 15° angles is needed (circular protractor).

• An arbitrary point on the sub-style line is chosen. From here, a long-line, at right-angles to it, is drawn. A line is drawn at right angles from the substyle height, so that it passes through that point. Its length is noted.
• The length is copied from the point to O'. This will become the centre used by circular protractor. Draw a line from here to crossing of the vertical and the long-line.
• The circular protractor is aligned so that zero falls on the new line. Points are marked off and lines drawn through them to the long line. From each of these crossings. a final line is drawn back to the Origin at the top. These are the hour-lines. 12 is on the vertical, and the forenoon hours are to the left- and the afternoon hours (fewer in number) to the right. ^[3]

Wigham-Richardson's method

Before the protractor became ubiquitous, compasses and the Scale of Chords were used for laying out an angle. This method originally used them.

• A large cross is drawn, ACB being the vertical line and PCQ horizontally.
• Two arcs are drawn to the right - AQ, and CT.
• Two triangle are drawn ACT- with the co-latitude (90- Φ) at the top, and CWX- with the declination 'D' at the centre. For the example these will be 38° and 20°

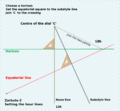
Finding SD

• A line is drawn from X through C to a point that will be eventually named S. Take compasses and using the radius CD swing an clockwise arc to this line, where it cuts is the point S. In otherwords CS is equal in length to CD.
• Drop a perpendicular line (RS) from line PQ to cut through S. To fix the point Y: copy the length RS, from C onto the line PQ. This is CY. RS=CY.
• Join A to Y. This is the substyle distance SD.

Finding SH and the centre of the equinoctial

• A long line, perpendicular to AY is drawn- it will take the points G,Y,P and M. YG is equal in length to CR. Join AG and the angle YAG is the substyle height.

Drawing the hourlines

At this point only three lines matter, the vertical, the substyle length and substyle height. A circle marked off in 15° angles is needed (circular protractor).

• A perpendicular line through Y is dropped from the sub-style line- the crossing is marked 'g '.
• Compasses are used to transfer this length onto the substyle line. The point is called 'O' ', this is the centre of the equinoctial circle- a long line F F' is drawn perpendicularly.
• Centre the circular protractor on O', with one line passing through P- call this XII.
• From A the actual hour-lines through each of the points (stars) where the protractor lines cross G,Y,P and M.^[4]

Use of Dialing rulers

Foster Serles Dialling Scales (1638) Foster is credited for producing a set of scales to assist in the laying out of the hour line on a dial. To use them SH and SD must already be known. The scales are placed on the SD line, and lines are drawn using the calculated SH value rather than the actual latitude.

Zarbula method

Zarbula is credited with the design of over a hundred sundials in Hautes Alpes and Piedmont. This region straddles the 45 ° parallel and as such his dials are a special case. He worked directly on the wall, and didn't require to know the latitude or the declination of the dial, these we found by observation. His dials were examples of frescos, and all gave five-minute accuracy..

Laying out the dial

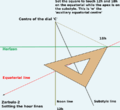
• With a plumb bob he drew a vertical line on the wall. This is the Noon Line.
• He hammered a rod into the wall at right angles to the vertical. This is known as the centre of the dial, C
• He observed and marked the shadow thrown by the tip of that rod, throughout a day. This line, technically known as a hyperbolic declination line.^{[lower-alpha 4]}
• Using a set of compasses, he determines the line of symmetry on the wall.^{[lower-alpha 5]} This is the substyle line.^{[lower-alpha 6]}

All the rest of the dial was laid out using a 45° square, with a 15° measure at the end. ^{[lower-alpha 7]}

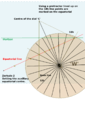
• He drew a horizontal line at a point of choice on the dial plate. This was the Horizon.
• The square was placed on the substyle facing outwards, it is slid into any convenient position where it cuts the horizon, and he drew a perpendicular line drawn to that point. This line is called the equatorial. A line was drawn from that point to the centre of the dial; it was the 18h line (or 6h depending on the declination (d) of the wall). The points where the equatorial crosses the noon line and where the equatorial crosses the substyle line were important.
• He placed apex of the square on the substyle line, so the sides passed through the equatorial points mentioned. (The 12h and 18h markers). The apex point is called the auxiliary equatorial centre.
• A protractor or squares ^{[lower-alpha 8]} drew off 15° intervals on the equatorial. These were connected to the centre of the dial: the hour lines. The distance from the auxiliary equatorial centre to the equatorial formed the substyle height at that point.^[5][6]

See also

• Schema for horizontal dials

References

Footnotes

Notes

Bibliography

• Waugh, Albert E. (1973). Sundials : their theory and construction. New York: Dover. ISBN 0486229475.  |access-date= requires |url= (help)

Time
Key concepts	Human Life Nature Past history deep time Present Future Futures studies Far future in religion Far future in science fiction and popular culture Timeline of the far future Eternity Eternity of the world
Measurement and standards	Chronometry UTC UT TAI Unit of time Planck time Second Minute Hour Day Week Month Year Decade Century Millennium Tropical year Sidereal year Measurement systems Time zone 12-hour clock 24-hour clock Daylight saving time Solar time Sidereal time Metric time Decimal time Hexadecimal time Calendars Gregorian Julian Hebrew Islamic Lunar Solar Hijri Mayan Intercalation Leap second Leap year
Clocks	Horology History of timekeeping devices Main types astrarium atomic quantum marine sundial sundial markup schema watch water-based
Chronology History	Astronomical chronology Big History Calendar era Chronicle Deep time Periodization Regnal year Timeline
Religion Mythology	Dreamtime Kāla Kalachakra Prophecy Time and fate deities Wheel of time Immortality
Philosophy of time	A-series and B-series B-theory of time Causality Duration Endurantism Eternal return Eternalism Event Perdurantism Presentism Temporal finitism Temporal parts The Unreality of Time
Human experience and use of time	Accounting period Chronemics Fiscal year Generation time Mental chronometry Music Procrastination Punctuality Temporal database Term Time discipline Time management Time perception Specious present Time-tracking software Time-use research Time-based currency (time banking) Time value of money Time clock Timesheet Yesterday
Time in	Geology Geological time age chron eon epoch era period Geochronology Geological history of Earth Physics Absolute time and space Arrow of time Chronon Coordinate time Imaginary time Planck epoch Planck time Proper time Rate Spacetime Theory of relativity Time dilation gravitational Time domain T-symmetry other subject areas Chronological dating Chronobiology Circadian rhythms Dating methodologies in archaeology Time geography
Related topics	Carpe diem Clock position Space System time Tempus fugit Time capsule Time complexity Time signature Time travel
Time portal