Rapidly-exploring random tree

Part of a series on
Probabilistic data structures
Bloom filter Count–min sketch Quotient filter Skip list
Random trees
Random binary tree Treap Rapidly exploring random tree
Related
Randomized algorithm
Computer science portal

A visualization of a RRT graph after 45 and 390 iterations

An animation of a RRT starting from iteration 0 to 10000

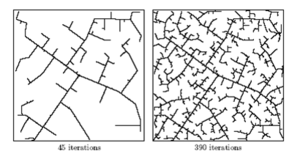
A rapidly exploring random tree (RRT) is an algorithm designed to efficiently search nonconvex, high-dimensional spaces by randomly building a space-filling tree. The tree is constructed incrementally from samples drawn randomly from the search space and is inherently biased to grow towards large unsearched areas of the problem. RRTs were developed by Steven M. LaValle and James J. Kuffner Jr. ^[1] .^[2] They easily handle problems with obstacles and differential constraints (nonholonomic and kinodynamic) and have been widely used in autonomous robotic motion planning.

RRTs can be viewed as a technique to generate open-loop trajectories for nonlinear systems with state constraints. An RRT can also be considered as a Monte-Carlo method to bias search into the largest Voronoi regions of a graph in a configuration space. Some variations can even be considered stochastic fractals.^[3]

Description

An RRT grows a tree rooted at the starting configuration by using random samples from the search space. As each sample is drawn, a connection is attempted between it and the nearest state in the tree. If the connection is feasible (passes entirely through free space and obeys any constraints), this results in the addition of the new state to the tree. With uniform sampling of the search space, the probability of expanding an existing state is proportional to the size of its Voronoi region. As the largest Voronoi regions belong to the states on the frontier of the search, this means that the tree preferentially expands towards large unsearched areas.

The length of the connection between the tree and a new state is frequently limited by a growth factor. If the random sample is further from its nearest state in the tree than this limit allows, a new state at the maximum distance from the tree along the line to the random sample is used instead of the random sample itself. The random samples can then be viewed as controlling the direction of the tree growth while the growth factor determines its rate. This maintains the space-filling bias of the RRT while limiting the size of the incremental growth.

RRT growth can be biased by increasing the probability of sampling states from a specific area. Most practical implementations of RRTs make use of this to guide the search towards the planning problem goals. This is accomplished by introducing a small probability of sampling the goal to the state sampling procedure. The higher this probability, the more greedily the tree grows towards the goal.

Algorithm

For a general configuration space C, the algorithm in pseudocode is as follows:

Algorithm BuildRRT
  Input: Initial configuration qinit, number of vertices in RRT K, incremental distance Δq)
  Output: RRT graph G

  G.init(qinit)
  for k = 1 to K
    qrand ← RAND_CONF()
    qnear ← NEAREST_VERTEX(qrand, G)
    qnew ← NEW_CONF(qnear, qrand, Δq)
    G.add_vertex(qnew)
    G.add_edge(qnear, qnew)
  return G

In the algorithm above, "RAND_CONF" grabs a random configuration q_rand in C. This may be replaced with a function "RAND_FREE_CONF" that uses samples in C_free, while rejecting those in C_obs using some collision detection algorithm.

"NEAREST_VERTEX" is a function that runs through all vertices v in graph G, calculates the distance between q_rand and v using some measurement function thereby returning the nearest vertex.

"NEW_CONF" selects a new configuration q_new by moving an incremental distance Δq from q_near in the direction of q_rand. (According to ^[4] in holonomic problems, this should be omitted and q_rand used instead of q_new.)

Variants and improvements for motion planning

• Parti-game directed RRTs (PDRRTs),^[5] a method that combines RRTs with the parti-game method^[6] to refine the search where it is needed (for example around obstacles) to be able to plan faster and solve more motion planning problems than RRT

It has been shown that, under 'mild technical conditions', the cost of the best path in the RRT converges almost surely to a non-optimal value.^[7] For that reason, it is desirable to find variants of the RRT that converges to the optimum:

• Rapidly-exploring random graph (RRG) and RRT*,^[7][8][9] a variant of RRT that converges towards an optimal solution
• RRT*-Smart,^[10] a method for accelerating the convergence rate of RRT* by using path optimization (in a similar fashion to Theta*) and intelligent sampling (by biasing sampling towards path vertices, which – after path optimization – are likely to be close to obstacles)
• A*-RRT and A*-RRT*,^[11] a two-phase motion planning method that uses a graph search algorithm to search for an initial feasible path in a low-dimensional space (not considering the complete state space) in a first phase, avoiding hazardous areas and preferring low-risk routes, which is then used to focus the RRT* search in the continuous high-dimensional space in a second phase
• RRT*FN,^[12][13][14] RRT* with a fixed number of nodes, which randomly removes a leaf node in the tree in every iteration
• RRT*-AR,^[15] sampling-based alternate routes planning
• Informed RRT*,^[16][17] improves the convergence speed of RRT* by introducing a heuristic, similar to the way in which A* improves upon Dijkstra's algorithm
• Real-Time RRT* (RT-RRT*),^[18] a variant of RRT* and informed RRT* that uses an online tree rewiring strategy that allows the tree root to move with the agent without discarding previously sampled paths, in order to obtain real-time path-planning in a dynamic environment such as a computer game
• Theta*-RRT,^[19] a two-phase motion planning method similar to A*-RRT* that uses a hierarchical combination of any-angle search with RRT motion planning for fast trajectory generation in environments with complex nonholonomic constraints

See also

• Any-angle path planning
• Probabilistic roadmap
• Space-filling tree
• Motion planning
• Randomized algorithm

References

External links

• Media related to Rapidly exploring random tree at Wikimedia Commons
• Java visualizer of RRT and RRT* including map editor