Quantum configuration space

In quantum mechanics, the Hilbert space is the space of complex-valued functions belonging to 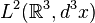$L^2 (\mathbb{R}^3 , d^3x)$ , where the simple 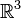$\mathbb{R}^3$ is the classical configuration space of free particle which has finite degrees of freedom, and 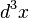$d^3 x$ is the Lebesgue measure on 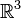$\mathbb{R}^3$ . 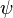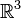In the quantum mechanics the domain space of the wave functions $\psi$ is the classical configuration space $\mathbb{R}^3$ .

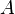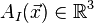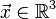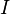In classical field theory, the configuration space of the field is an infinite-dimensional space. The single point denoted $A$ in this space is represented by the set of functions $A_I (\vec{x}) \in \mathbb{R}^3$ where $\vec{x} \in \mathbb{R}^3$ and $I$ represents an index set.

In quantum field theory, it is expected that the Hilbert space is also the 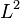$L^2$ space on the configuration space of the field, which is infinite dimensional, with respect to some Borel measure naturally defined. However, it is often hard to define a concrete Borel measure on the classical configuration space, since the integral theory on infinite dimensional space is involved.^[1]

Thus the intuitive expectation should be modified, and the concept of quantum configuration space should be introduced as a suitable enlargement of the classical configuration space so that an infinite dimensional measure, often a cylindrical measure, can be well defined on it.

In quantum field theory, the quantum configuration space, the domain of the wave functions 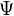$\Psi$ , is larger than the classical configuration space. While in the classical theory we can restrict ourselves to suitably smooth fields, in quantum field theory we are forced to allow distributional field configurations. In fact, in quantum field theory physically interesting measures are concentrated on distributional configurations.

That physically interesting measures are concentrated on distributional fields is the reason why in quantum theory fields arise as operator-valued distributions.^[2]

The example of a scalar field can be found in the references ^[3]^[4]

References

↑ Y. Choquet-Bruhat, C. Dewitt-Morette, M. Dillard-Bleick, Analysis, Manifold, and Physics, (North-Holland Publishing Company, 1977).
↑ Conceptual Foundations of Quantum Field Theory By Tian Yu Cao
↑ A. Ashtekar and J. Lewandowski, Background independent quantum gravity: A status report, Class. Quantum Grav. 21, R53 (2004), (preprint: gr-qc/0404018).
↑ A. Ashtekar, J. Lewandowski, D. Marolf, J. Mour ̃ao, and T. Thiemann, A manifestly gauge-invariant approach to quantum theories of gauge fields, (preprint: hep-th/9408108).

This article is issued from Wikipedia - version of the 11/30/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.