Parallelogon

A parallelogon is constructed by two or three pairs of parallel line segments. The vertices and edges on the interior of the hexagon are suppressed.
There are five Bravais lattices in two dimensions, related to the parallelogon tessellations by their five symmetry variations.

A parallelogon is a polygon such that images of the polygon under translations only tile the plane when fitted together along entire sides.[1]

A parallelogon must have an even number of sides and opposite sides must be equal in length and parallel (hence the name). A less obvious restriction is that a parallelogon can only have four or six sides;[1] a four-sided parallelogon is a parallelogram. In general a parallelogon has 180-degree rotational symmetry around its center.

Two polygonal types

Quadrilateral and hexagonal parallelogons each have varied geometric symmetric forms. In general they all have central inversion symmetry, order 2. Hexagonal parallelogons enable the possibility of nonconvex polygons.

SidesExamplesNameSymmetry
4 ParallelogramZ2, order 2
Rectangle & rhombusDih2, order 4
SquareDih4, order 8
6 Elongated
parallelogram 		Z2, order 2
Elongated
rhombus		Dih2, order 4
Regular
hexagon 		Dih6, order 12

Geometric variations

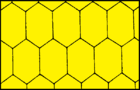
Parallelogram can tile the plane as a distorted square tiling while hexagonal parallelogon can tiling the plane as a distorted regular hexagonal tiling.

Parallelogram tilings
1 length 2 lengths
Right Skew Right Skew

Square
p4m (*442)
Rhombus
cmm (2*22)
Rectangle
pmm (*2222)
Parallelogram
p2 (2222)
Hexagonal parallelogon tilings
1 length 2 lengths 3 lengths
Regular hexagon
p6m (*632)		 Elongated rhombus
cmm (2*22)		 Elongated parallelogram
p2 (2222)

See also

References

  1. 1 2 Aleksandr Danilovich Aleksandrov Convex Polyhedra p351
This article is issued from Wikipedia - version of the 11/14/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.