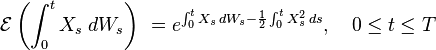Novikov's condition

In probability theory, Novikov's condition is the sufficient condition for a stochastic process which takes the form of the Radon-Nikodym derivative in Girsanov's theorem to be a martingale. If satisfied together with other conditions, Girsanov's theorem may be applied to a Brownian motion stochastic process to change from the original measure to the new measure defined by the Radon-Nikodym derivative.

This condition was suggested and proved by Alexander Novikov. There are other results which may be used to show that the Radon-Nikodym derivative is a martingale, such as the more general criterion Kazamaki's condition, however Novikov's condition is the most well-known result.

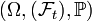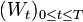Assume that $(X_t)_{0\leq t\leq T}$ is a real valued adapted process on the probability space $\left (\Omega, (\mathcal{F}_t), \mathbb{P}\right)$ and $(W_t)_{0\leq t\leq T}$ is an adapted Brownian motion:^[1]^:334

If the condition

\mathbb{E}\left[e^{\frac12\int_0^T|X|_t^2\,dt} \right]<\infty

is fulfilled then the process

\ \mathcal{E}\left( \int_0^t X_s \; dW_s \right) \ = e^{\int_0^t X_s\, dW_s -\frac{1}{2}\int_0^t X_s^2\, ds},\quad 0\leq t\leq T

is a martingale under the probability measure 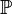$\mathbb{P}$ and the filtration 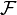$\mathcal{F}$ . Here 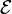$\mathcal{E}$ denotes the Doléans-Dade exponential.

References

↑ Pascucci, Andrea (2011) PDE and Martingale Methods in Option Pricing. Berlin: Springer-Verlag

Comments on Girsanov's Theorem by H. E. Krogstad, IMF 2003

This article is issued from Wikipedia - version of the 8/30/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.