Non-expanding horizon
A non-expanding horizon (NEH) is an enclosed null surface whose intrinsic structure is preserved. An NEH is the geometric prototype of an isolated horizon which describes a black hole in equilibrium with its exterior from the quasilocal perspective. It is based on the concept and geometry of NEHs that the two quasilocal definitions of black holes, weakly isolated horizons and isolated horizons, are developed.
Definition of NEHs
A three-dimensional submanifold ∆ is defined as a generic (rotating and distorted) NEH if it respects the following conditions:[1][2][3]
(i) ∆ is null and topologically 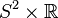 ;
;
(ii) Along any null normal field 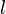 tangent to ∆, the outgoing expansion rate
tangent to ∆, the outgoing expansion rate 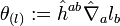 vanishes;
vanishes;
(iii) All field equations hold on ∆, and the stress–energy tensor 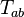 on ∆ is such that
on ∆ is such that 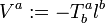 is a future-directed causal vector (
is a future-directed causal vector (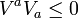 ) for any future-directed null normal
) for any future-directed null normal 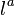 .
.
Condition (i) is fairly trivial and just states the general fact that from a 3+1 perspective[4] an NEH ∆ is foliated by spacelike 2-spheres ∆'=S2, where S2 emphasizes that ∆' is topologically compact with genus zero (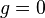 ). The signature of ∆ is (0,+,+) with a degenerate temporal coordinate, and the intrinsic geometry of a foliation leaf ∆'=S2 is nonevolutional. The property
). The signature of ∆ is (0,+,+) with a degenerate temporal coordinate, and the intrinsic geometry of a foliation leaf ∆'=S2 is nonevolutional. The property 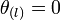 in condition (ii) plays a pivotal role in defining NEHs and the rich implications encoded therein will be extensively discussed below. Condition (iii) makes one feel free to apply the Newman–Penrose (NP) formalism[5][6] of Einstein-Maxwell field equations to the horizon and its near-horizon vicinity; furthermore, the very energy inequality is motivated from the dominant energy condition[7] and is a sufficient condition for deriving many boundary conditions of NEHs.
in condition (ii) plays a pivotal role in defining NEHs and the rich implications encoded therein will be extensively discussed below. Condition (iii) makes one feel free to apply the Newman–Penrose (NP) formalism[5][6] of Einstein-Maxwell field equations to the horizon and its near-horizon vicinity; furthermore, the very energy inequality is motivated from the dominant energy condition[7] and is a sufficient condition for deriving many boundary conditions of NEHs.
Note: In this article, following the convention set up in refs.,[1][2][3] "hat" over the equality symbol 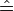 means equality on the black-hole horizons (NEHs), and "hat" over quantities and operators (
means equality on the black-hole horizons (NEHs), and "hat" over quantities and operators ( ,
,  , etc.) denotes those on a foliation leaf of the horizon. Also, ∆ is the standard symbol for both an NEH and the directional derivative ∆
, etc.) denotes those on a foliation leaf of the horizon. Also, ∆ is the standard symbol for both an NEH and the directional derivative ∆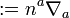 in NP formalism, and we believe this won't cause an ambiguity.
in NP formalism, and we believe this won't cause an ambiguity.
Boundary conditions implied by the definition
Now let's work out the implications of the definition of NEHs, and these results will be expressed in the language of NP formalism with the convention[5][6] 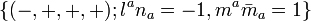 (Note: unlike the original convention[8][9]
(Note: unlike the original convention[8][9] 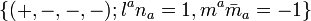 , this is the usual one employed in studying trapped null surfaces and quasilocal definitions of black holes[10]). Being a null normal to ∆,
, this is the usual one employed in studying trapped null surfaces and quasilocal definitions of black holes[10]). Being a null normal to ∆, 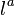 is automatically geodesic,
is automatically geodesic, 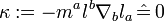 , and twist free,
, and twist free, 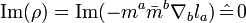 . For an NEH, the outgoing expansion rate
. For an NEH, the outgoing expansion rate 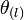 along
along 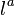 is vanishing,
is vanishing, 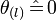 , and consequently
, and consequently 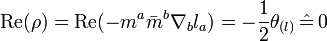 . Moreover, according to the Raychaudhuri-NP expansion-twist equation,[11]
. Moreover, according to the Raychaudhuri-NP expansion-twist equation,[11]
it follows that on ∆
where 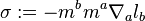 is the NP-shear coefficient. Due to the assumed energy condition (iii), we have
is the NP-shear coefficient. Due to the assumed energy condition (iii), we have 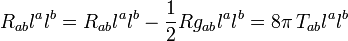 (
( ), and therefore
), and therefore  is nonnegative on ∆. The product
is nonnegative on ∆. The product  is of course nonnegative, too. Consequently,
is of course nonnegative, too. Consequently,  and
and 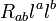 must be simultaneously zero on ∆, i.e.
must be simultaneously zero on ∆, i.e. 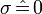 and
and  . As a summary,
. As a summary,
Thus, the isolated horizon ∆ is nonevolutional and all foliation leaves ∆'=S2 look identical with one another. The relation 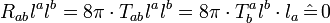 implies that the causal vector
implies that the causal vector 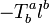 in condition (iii) is proportional to
in condition (iii) is proportional to 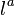 and
and 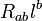 is proportional to
is proportional to 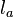 on the horizon ∆; that is,
on the horizon ∆; that is,  and
and 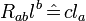 ,
, 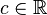 . Applying this result to the related Ricci-NP scalars, we get
. Applying this result to the related Ricci-NP scalars, we get 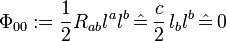 , and
, and 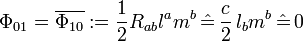 , thus
, thus
The vanishing of Ricci-NP scalars 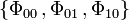 signifies that, there is no energy–momentum flux of any kind of charge across the horizon, such as electromagnetic waves, Yang–Mills flux or dilaton flux. Also, there should be no gravitational waves crossing the horizon; however, gravitational waves are propagation of perturbations of the spacetime continuum rather than flows of charges, and therefore depicted by four Weyl-NP scalars
signifies that, there is no energy–momentum flux of any kind of charge across the horizon, such as electromagnetic waves, Yang–Mills flux or dilaton flux. Also, there should be no gravitational waves crossing the horizon; however, gravitational waves are propagation of perturbations of the spacetime continuum rather than flows of charges, and therefore depicted by four Weyl-NP scalars 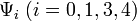 (excluding
(excluding 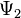 ) rather than Ricci-NP quantities
) rather than Ricci-NP quantities 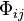 .[5] According to the Raychaudhuri-NP shear equation[11]
.[5] According to the Raychaudhuri-NP shear equation[11]
or the NP field equation on the horizon
it follows that  . Moreover, the NP equation
. Moreover, the NP equation
implies that 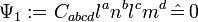 . To sum up, we have
. To sum up, we have
which means that,[5] geometrically, a principal null direction of Weyl's tensor is repeated twice and 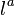 is aligned with the principal direction; physically, no gravitational waves (transverse component
is aligned with the principal direction; physically, no gravitational waves (transverse component 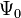 and longitudinal component
and longitudinal component  ) enter the black hole. This result is consistent with the physical scenario defining NEHs.
) enter the black hole. This result is consistent with the physical scenario defining NEHs.
Remarks: Spin coefficients related to Raychaudhuri's equation
For a better understanding of the previous section, we will briefly review the meanings of relevant NP spin coefficients in depicting null congruences.[7] The tensor form of Raychaudhuri's equation[12] governing null flows reads
where 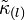 is defined such that
is defined such that 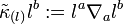 . The quantities in Raychaudhuri's equation are related with the spin coefficients via[5][13][14]
. The quantities in Raychaudhuri's equation are related with the spin coefficients via[5][13][14]
- where Eq(10) follows directly from
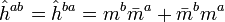 and
and
Moreover, a null congruence is hypersurface orthogonal if 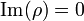 .[5]
.[5]
Constraints from electromagnetic fields
Vacuum NEHs on which 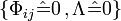 are the simplest types of NEHs, but in general there can be various physically meaningful fields surrounding an NEH, among which we are mostly interested in electrovacuum fields with
are the simplest types of NEHs, but in general there can be various physically meaningful fields surrounding an NEH, among which we are mostly interested in electrovacuum fields with 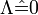 . This is the simplest extension of vacuum NEHs, and the nonvanishing energy-stress tensor for electromagnetic fields reads
. This is the simplest extension of vacuum NEHs, and the nonvanishing energy-stress tensor for electromagnetic fields reads
where 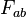 refers to the antisymmetric (
refers to the antisymmetric ( ,
, 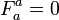 ) electromagnetic field strength, and
) electromagnetic field strength, and 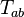 is trace-free (
is trace-free (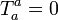 ) by definition and respects the dominant energy condition. (One should be careful with the antisymmetry of
) by definition and respects the dominant energy condition. (One should be careful with the antisymmetry of 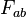 in defining Maxwell-NP scalars
in defining Maxwell-NP scalars 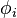 ).
).
The boundary conditions derived in the previous section are applicable to generic NEHs. In the electromagnetic case, 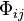 can be specified in a more particular way. By the NP formalism of Einstein-Maxwell equations, one has[5]
can be specified in a more particular way. By the NP formalism of Einstein-Maxwell equations, one has[5]
where 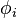 denote the three Maxwell-NP scalars. As an alternative to Eq(), we can see that the condition
denote the three Maxwell-NP scalars. As an alternative to Eq(), we can see that the condition 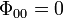 also results from the NP equation
also results from the NP equation
- as
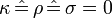 , so
, so
It follows straightforwardly that
These results demonstrate that, there are no electromagnetic waves across (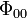 ,
, 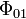 ) or along (\Phi_{02}) the NEH except the null geodesics generating the horizon. It is also worthwhile to point out that, the supplementary equation
) or along (\Phi_{02}) the NEH except the null geodesics generating the horizon. It is also worthwhile to point out that, the supplementary equation 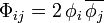 in Eq() is only valid for electromagnetic fields; for example, in the case of Yang–Mills fields there will be
in Eq() is only valid for electromagnetic fields; for example, in the case of Yang–Mills fields there will be 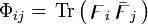 where
where 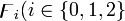 are Yang–Mills-NP scalars.[15]
are Yang–Mills-NP scalars.[15]
Adapted tetrad on NEHs and further properties
Usually, null tetrads adapted to spacetime properties are employed to achieve the most succinct NP descriptions. For example, a null tetrad can be adapted to principal null directions once the Petrov type is known; also, at some typical boundary regions such as null infinity, timelike infinity, spacelike infinity, black hole horizons and cosmological horizons, tetrads can be adapted to boundary structures. Similarly, a preferred tetrad[1][2][3] adapted to on-horizon geometric behaviors is employed in the literature to further investigate NEHs.
As indicated from the 3+1 perspective from condition (i) in the definition, an NEH ∆ is foliated by spacelike hypersurfaces ∆'=S2 transverse to its null normal along an ingoing null coordinate 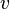 , where we follow the standard notation of ingoing Eddington–Finkelstein null coordinates and use
, where we follow the standard notation of ingoing Eddington–Finkelstein null coordinates and use 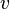 to label the 2-dimensional leaves
to label the 2-dimensional leaves 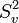 at
at 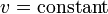 ; that is, ∆=∆'×[v0,v1]=S2×[v0,v1].
; that is, ∆=∆'×[v0,v1]=S2×[v0,v1]. 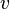 is set to be future-directed and choose the first tetrad covector
is set to be future-directed and choose the first tetrad covector 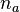 as
as 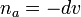 ,[2][3] and then there will be a unique vector field
,[2][3] and then there will be a unique vector field 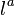 as null normals to
as null normals to 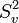 satisfying the cross-normalization
satisfying the cross-normalization 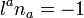 and affine parametrization
and affine parametrization 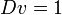 ; such choice of
; such choice of 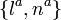 would actually yields a preferred foliation of ∆. While
would actually yields a preferred foliation of ∆. While 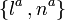 are related to the extrinsic properties and null generators (i.e. null flows/geodesic congruence on ∆), the remaining two complex null vectors
are related to the extrinsic properties and null generators (i.e. null flows/geodesic congruence on ∆), the remaining two complex null vectors 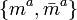 are to span the intrinsic geometry of a foliation leaf
are to span the intrinsic geometry of a foliation leaf 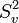 , tangent to ∆ and transverse to
, tangent to ∆ and transverse to 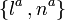 ; that is,
; that is, 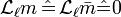 .
.
Now let's check the consequences of this kind of adapted tetrad. Since
with 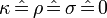 , we have
, we have
Also, in such an adapted frame, the derivative 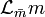 on ∆'×[v0,v1]=S2×[v0,v1] should be purely intrinsic; thus in the commutator
on ∆'×[v0,v1]=S2×[v0,v1] should be purely intrinsic; thus in the commutator
the coefficients for the directional derivatives 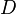 and ∆ must be zero, that is
and ∆ must be zero, that is
so the ingoing null normal field 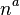 is twist-free by
is twist-free by  , and
, and  equals the ingoing expansion rate
equals the ingoing expansion rate  .
.
Discussion
So far, the definition and boundary conditions of NEHs have been introduced. The boundary conditions include those for an arbitrary NEH, specific characteristics for Einstein-Maxwell (electromagnetic) NEHs, as well as further properties in an adapted tetrad. Based on NEHs, WIHs which have valid surface gravity can be defined to generalize the black hole mechanics. WIHs are sufficient in studying the physics on the horizon, but for geometric purposes,[2] stronger restrictions can be imposed to WIHs so as to introduce IHs, where the equivalence class of null normals ![[\ell]](../I/m/617a11bbf9c9843456e232feb6040e09.png) fully preserves the induced connection
fully preserves the induced connection 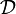 on the horizon.
on the horizon.
References
- 1 2 3 Abhay Ashtekar, Christopher Beetle, Olaf Dreyer, et al. "Generic isolated horizons and their applications". Physical Review Letters, 2000, 85(17): 3564-3567. arXiv:gr-qc/0006006v2
- 1 2 3 4 5 Abhay Ashtekar, Christopher Beetle, Jerzy Lewandowski. "Geometry of generic isolated horizons". Classical and Quantum Gravity, 2002, 19(6): 1195-1225. arXiv:gr-qc/0111067v2
- 1 2 3 4 Abhay Ashtekar, Stephen Fairhurst, Badri Krishnan. "Isolated horizons: Hamiltonian evolution and the first law". Physical Review D, 2000, 62(10): 104025. gr-qc/0005083
- ↑ Thomas W Baumgarte, Stuart L Shapiro. Numerical Relativity: Solving Einstein's Equations on the Computer. Cambridge: Cambridge University Press, 2010. Chapter 2: The 3+1 decomposition of Einstein's equations, page 23.
- 1 2 3 4 5 6 7 Jeremy Bransom Griffiths, Jiri Podolsky. Exact Space-Times in Einstein's General Relativity. Cambridge: Cambridge University Press, 2009. Chapter 2.
- 1 2 Valeri P Frolov, Igor D Novikov. Black Hole Physics: Basic Concepts and New Developments. Berlin: Springer, 1998. Appendix E.
- 1 2 Eric Poisson. A Relativist's Toolkit: The Mathematics of Black-Hole Mechanics. Cambridge: Cambridge University Press, 2004. Chapters 2 and 3.
- ↑ Ezra T Newman, Roger Penrose. "An Approach to Gravitational Radiation by a Method of Spin Coefficients". Journal of Mathematical Physics, 1962, 3(3): 566-768.
- ↑ Ezra T Newman, Roger Penrose. "Errata: An Approach to Gravitational Radiation by a Method of Spin Coefficients". Journal of Mathematical Physics, 1963, 4(7): 998.
- ↑ Ivan Booth. "Black hole boundaries". Canadian Journal of Physics, 2005, 83(11): 1073-1099. [arxiv.org/abs/gr-qc/0508107 arXiv:gr-qc/0508107v2]
- 1 2 Subrahmanyan Chandrasekhar. The Mathematical Theory of Black Holes. Chicago: University of Chicago Press, 1983. Section 9(a), page 56.
- ↑ Sayan Kar, Soumitra SenGupta. The Raychaudhuri equations: a brief review. Pramana, 2007, 69(1): 49-76. [arxiv.org/abs/gr-qc/0611123v1 gr-qc/0611123]
- ↑ David McMahon. Relativity Demystified - A Self-Teaching Guide. New York: McGraw-Hill, 2006. Chapter 9.
- ↑ Alex Nielsen. PhD thesis: Black Hole Horizons and Black Hole Thermodynamics. University of Canterbury, 2007. Section 2.3. Available online: http://ir.canterbury.ac.nz/handle/10092/1363.
- ↑ E T Newman, K P Tod. Asymptotically Flat Spacetimes. page 27, Appendix A.2. In A Held (Editor): General relativity and gravitation: one hundred years after the birth of Albert Einstein. Vol(2). New York and London: Plenum Press, 1980.
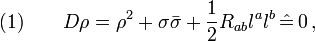
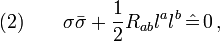

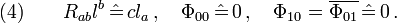
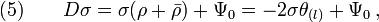
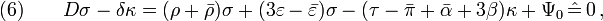



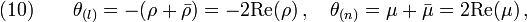
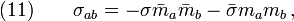
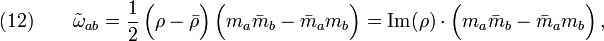
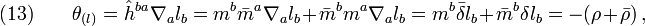
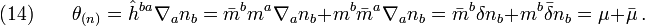
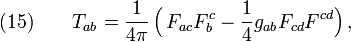
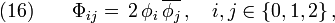
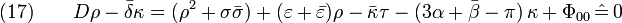


![(20)\qquad \mathcal{L}_{\ell}m=[\ell,m]\,\hat{=}\,0\;\Rightarrow\; \delta D-D\delta=(\bar{\alpha}+\beta-\bar{\pi})D+\kappa_{}\Delta-(\bar{\rho}+\varepsilon-\bar{\varepsilon})\delta-\sigma\bar{\delta} \,\hat{=}\,0 \,,](../I/m/eeb2a61802becb66198ed3350171a9a7.png)
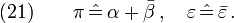
![(22)\qquad \mathcal{L}_{\bar{m}}m=[\bar{m}, m]=\bar{\delta}\delta-\delta\bar{\delta}=
(\bar{\mu}-\mu)D+(\bar{\rho}-\rho)\Delta-(\bar{\beta}-\alpha)\delta-(\bar{\alpha}-\beta)\bar{\delta}\,,](../I/m/e318490f2959dab6b0051eadf841ccca.png)
