Natural pseudodistance
In size theory, the natural pseudodistance between two size pairs 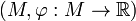 ,
, 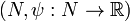 is the value
is the value 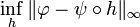 , where
, where 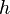 varies in the set of all homeomorphisms from the manifold
varies in the set of all homeomorphisms from the manifold 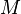 to the manifold
to the manifold 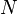 and
and 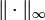 is the supremum norm. If
is the supremum norm. If 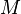 and
and 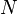 are not homeomorphic, then the natural pseudodistance is defined to be
are not homeomorphic, then the natural pseudodistance is defined to be 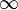 .
It is usually assumed that
.
It is usually assumed that 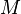 ,
, 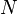 are
are 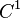 closed manifolds and the measuring functions
closed manifolds and the measuring functions 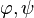 are
are 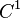 . Put another way, the natural pseudodistance measures the infimum of the change of the measuring function induced by the homeomorphisms from
. Put another way, the natural pseudodistance measures the infimum of the change of the measuring function induced by the homeomorphisms from 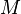 to
to 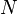 .
.
The concept of natural pseudodistance can be easily extended to size pairs where the measuring function 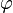 takes values in
takes values in 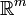 .[1]
.[1]
Main properties
It can be proved [2]
that the natural pseudodistance always equals the Euclidean distance between two critical values of the measuring functions (possibly, of the same measuring function) divided by a suitable positive integer 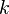 .
If
.
If 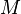 and
and 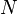 are surfaces, the number
are surfaces, the number 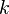 can be assumed to be
can be assumed to be 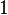 ,
, 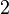 or
or 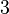 .[3] If
.[3] If 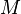 and
and 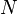 are curves, the number
are curves, the number 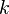 can be assumed to be
can be assumed to be 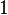 or
or 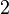 .[4]
If an optimal homeomorphism
.[4]
If an optimal homeomorphism 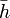 exists (i.e.,
exists (i.e., 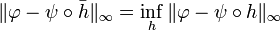 ), then
), then 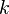 can be assumed to be
can be assumed to be 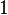 .[2]
.[2]
See also
References
- ↑ Patrizio Frosini, Michele Mulazzani, Size homotopy groups for computation of natural size distances, Bulletin of the Belgian Mathematical Society, 6:455-464, 1999.
- 1 2 Pietro Donatini, Patrizio Frosini, Natural pseudodistances between closed manifolds, Forum Mathematicum, 16(5):695-715, 2004.
- ↑ Pietro Donatini, Patrizio Frosini, Natural pseudodistances between closed surfaces, Journal of the European Mathematical Society, 9(2):231–253, 2007.
- ↑ Pietro Donatini, Patrizio Frosini, Natural pseudodistances between closed curves, Forum Mathematicum, 21(6):981–999, 2009.