Maxwell relations
| Thermodynamics | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
The classical Carnot heat engine | ||||||||||||
|
Branches |
||||||||||||
|
||||||||||||
| Book:Thermodynamics | ||||||||||||
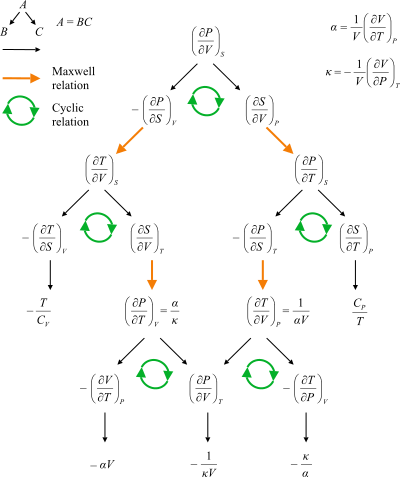
Maxwell's relations are a set of equations in thermodynamics which are derivable from the symmetry of second derivatives and from the definitions of the thermodynamic potentials. These relations are named for the nineteenth-century physicist James Clerk Maxwell.
Equations
The structure of Maxwell relations is a statement of equality among the second derivatives for continuous functions. It follows directly from the fact that the order of differentiation of an analytic function of two variables is irrelevant (Schwarz theorem). In the case of Maxwell relations the function considered is a thermodynamic potential and xi and xj are two different natural variables for that potential:
Schwarz' theorem (general)
where the partial derivatives are taken with all other natural variables held constant. It is seen that for every thermodynamic potential there are n(n − 1)/2 possible Maxwell relations where n is the number of natural variables for that potential.
The four most common Maxwell relations
The four most common Maxwell relations are the equalities of the second derivatives of each of the four thermodynamic potentials, with respect to their thermal natural variable (temperature T; or entropy S) and their mechanical natural variable (pressure P; or volume V):
Maxwell's relations (common)
where the potentials as functions of their natural thermal and mechanical variables are the internal energy U(S, V), enthalpy H(S, P), Helmholtz free energy F(T, V) and Gibbs free energy G(T, P). The thermodynamic square can be used as a mnemonic to recall and derive these relations. The usefulness of these relations lies in their quantifying entropy changes, which are not directly measurable, in terms of measurable quantities like temperature, volume, and pressure.
Derivation
Maxwell relations are based on simple partial differentiation rules, in particular the total differential of a function and the symmetry of evaluating second order partial derivatives.
Derivation Derivation of the Maxwell relation can be deduced from the differential forms of the thermodynamic potentials: The differential form of internal energy U is
This equation resembles total differentials of the form
It can be shown that for any equation of the form
that
Consider, the equation . We can now immediately see that
Since we also know that for functions with continuous second derivatives, the mixed partial derivatives are identical (Symmetry of second derivatives), that is, that
we therefore can see that
and therefore that
Derivation of Maxwell Relation from Helmholtz Free energy
- The differential form of Helmholtz free energy is
From symmetry of second derivatives
and therefore that
The other two Maxwell relations can be derived from differential form of enthalpy and the differential form of Gibbs free energy in a similar way. So all Maxwell Relationships above follow from one of the Gibbs equations.
Extended derivation Combined form first and second law of thermodynamics, - (Eq.1)
U, S, and V are state functions. Let,
Substitute them in Eq.1 and one gets,
And also written as,
comparing the coefficient of dx and dy, one gets
Differentiating above equations by y, x respectively
- (Eq.2)
- and
- (Eq.3)
U, S, and V are exact differentials, therefore,
Subtract eqn(2) and (3) and one gets
- Note: The above is called the general expression for Maxwell's thermodynamical relation.
- Maxwell's first relation
- Allow x = S and y = V and one gets
- Maxwell's second relation
- Allow x = T and y = V and one gets
- Maxwell's third relation
- Allow x = S and y = P and one gets
- Maxwell's fourth relation
- Allow x = T and y = P and one gets
- Maxwell's fifth relation
- Allow x = P and y = V
- = 1
- Maxwell's sixth relation
- Allow x = T and y = S and one gets
- = 1
General Maxwell relationships
The above are not the only Maxwell relationships. When other work terms involving other natural variables besides the volume work are considered or when the number of particles is included as a natural variable, other Maxwell relations become apparent. For example, if we have a single-component gas, then the number of particles N is also a natural variable of the above four thermodynamic potentials. The Maxwell relationship for the enthalpy with respect to pressure and particle number would then be:
where μ is the chemical potential. In addition, there are other thermodynamic potentials besides the four that are commonly used, and each of these potentials will yield a set of Maxwell relations.
Each equation can be re-expressed using the relationship
which are sometimes also known as Maxwell relations.
