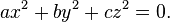Legendre's equation
You might be looking for Legendre's differential equation.
In mathematics, Legendre's equation is the Diophantine equation
The equation is named for Adrien Marie Legendre who proved in 1785 that it is solvable in integers x, y, z, not all zero, if and only if −bc, −ca and −ab are quadratic residues modulo a, b and c, respectively, where a, b, c are nonzero, square-free, pairwise relatively prime integers, not all positive or all negative .
References
- L. E. Dickson, History of the Theory of Numbers. Vol.II: Diophantine Analysis, Chelsea Publishing, 1971, ISBN 0-8284-0086-5. Chap.XIII, p. 422.
- J.E. Cremona and D. Rusin, "Efficient solution of rational conics", Math. Comp., 72 (2003) pp. 1417-1441.
This article is issued from Wikipedia - version of the 10/5/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.