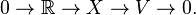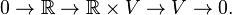K-space (functional analysis)

In mathematics, more specifically in functional analysis, a K-space is an F-space 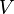$V$ such that every extension of F-spaces (or twisted sum) of the form

0\rightarrow \mathbb R\rightarrow X\rightarrow V\rightarrow 0. \,\!

is equivalent to the trivial one^[1]

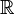0\rightarrow \mathbb R\rightarrow \mathbb R\times V \rightarrow V\rightarrow 0. \,\!

where $\mathbb R$ is the real line.

Examples

Finite dimensional Banach spaces are K-spaces.
The 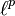$\ell^p$ spaces for 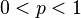$0< p < 1$ are K-spaces.^[1]
N. J. Kalton and N. P. Roberts proved that the Banach space 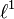$\ell^1$ is not a K-space.^[1]

References

1 2 3 Kalton, N. J.; Peck, N. T.; Roberts, James W. An F-space sampler. London Mathematical Society Lecture Note Series, 89. Cambridge University Press, Cambridge, 1984. xii+240 pp. ISBN 0-521-27585-7

This article is issued from Wikipedia - version of the 5/18/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.