Internal model (motor control)

Forward model of an arm movement. The motor command, u(t), of the arm movement is input to the plant and the predicted position of the body, x̃(t), is output.

In the subject area of control theory, an internal model is a process that simulates the response of the system in order to estimate the outcome of a system disturbance. The internal model principle was first articulated in 1976 by B. A. Francis and W. M. Wonham^[1] as an explicit formulation of the Conant and Ashby good regulator theorem. ^[2] It stands in contrast to classical control, in that the classical feedback loop fails to explicitly model the controlled system (although the classical controller may contain an implicit model).^[3][4]

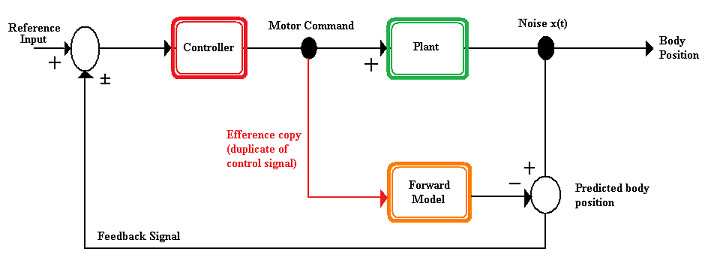
The internal model theory of motor control argues that the motor system is controlled by the constant interactions of the “plant” and the “controller.” The plant is the body part being controlled, while the internal model itself is considered part of the controller. Information from the controller, such as information from the CNS, feedback information, and the efference copy, is sent to the plant which moves accordingly.

Internal models can be controlled through either feed-forward or feedback control. Feed-forward control computes its input into a system using only the current state and its model of the system. It does not use feedback, so it cannot correct for errors in its control. In feedback control, some of the output of the system can be fed back into the system’s input, and the system is then able to make adjustments or compensate for errors from its desired output. Two primary types of internal models have been proposed: forward models and inverse models. In simulations, models can be combined together to solve more complex movement tasks.

Forward models

Figure 1. The desired position of the body is the reference input to the hypothetical controller, which generates the necessary motor command. This motor command is sent to the plant to move the body and an efference copy of the motor command is sent to a forward model. The output from the forward model (predicted body position) is compared with the output from the plant (body position). Noise from the system or the environment may cause differences between the actual and predicted body positions. The error (difference) between the actual and predicted positions can provide feedback to improve the movement for the next iteration of the internal model.

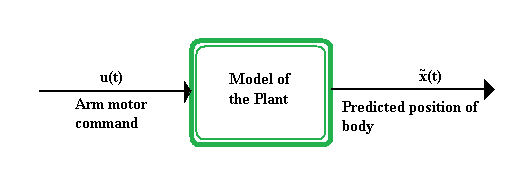
In their simplest form, forward models take the input of a motor command to the “plant” and output a predicted position of the body.

The motor command input to the forward model can be an efference copy, as seen in Figure 1. The output from that forward model, the predicted position of the body, is then compared with the actual position of the body. The actual and predicted position of the body may differ due to noise introduced into the system by either internal (e.g. body sensors are not perfect, sensory noise) or external (e.g. unpredictable forces from outside the body) sources. If the actual and predicted body positions differ, the difference can be fed back as an input into the entire system again so that an adjusted set of motor commands can be formed to create a more accurate movement.

Inverse models

Figure 2. Inverse model of a reaching task. The arm’s desired trajectory, Xref(t), is input into the model, which generates the necessary motor commands, ũ(t), to control the arm.

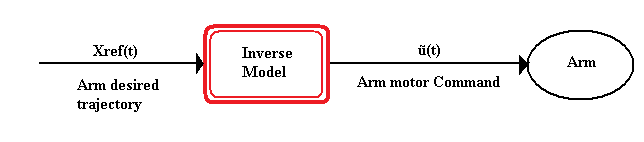
Inverse models use the desired and actual position of the body as inputs to estimate the necessary motor commands which would transform the current position into the desired one. For example, in an arm reaching task, the desired position (or a trajectory of consecutive positions) of the arm is input into the postulated inverse model, and the inverse model generates the motor commands needed to control the arm and bring it into this desired configuration (Figure 2). Inverse internal models are also in close connection with the uncontrolled manifold hypothesis (UCM), see also here.

Combined forward and inverse models

Theoretical work has shown that in models of motor control, when inverse models are used in combination with a forward model, the efference copy of the motor command output from the inverse model can be used as an input to a forward model for further predictions. For example if, in addition to reaching with the arm, the hand must be controlled to grab an object, an efference copy of the arm motor command can be input into a forward model to estimate the arm's predicted trajectory. With this information, the controller can then generate the appropriate motor command telling the hand to grab the object. It has been proposed that if they exist, this combination of inverse and forward models would allow the CNS to take a desired action (reach with the arm), accurately control the reach and then accurately control the hand to grip an object.^[5]

Adaptive Control theory

With the assumption that new models can be acquired and pre-existing models can be updated, the efference copy is important for the adaptive control of a movement task. Throughout the duration of a motor task, an efference copy is fed into a forward model known as a dynamics predictor whose output allows prediction of the motor output. When applying adaptive control theory techniques to motor control, efference copy is used in indirect control schemes as the input to the reference model.

Scientists

A wide range of scientists contribute to progress on the internal model hypothesis. Michael I. Jordan, Emmanuel Todorov and Daniel Wolpert contributed significantly to the mathematical formalization. Sandro Mussa-Ivaldi, Mitsuo Kawato, Claude Ghez, Reza Shadmehr, Randy Flanagan and Konrad Kording contributed with numerous behavioral experiments. The DIVA model of speech production developed by Frank H. Guenther and colleagues uses combined forward and inverse models to produce auditory trajectories with simulated speech articulators. Two interesting inverse internal models for the control of speech production^[6] were developed by Iaroslav Blagouchine & Eric Moreau.^[7] Both models combine the optimum principles and the equilibrium-point hypothesis (motor commands λ are taken as coordinates of the internal space). The input motor command λ is found by minimizing the length of the path traveled in the internal space, either under the acoustical constraint (the first model), or under the both acoustical and mechanical constraints (the second model). The acoustical constraint is related to the quality of the produced speech (measured in terms of formants), while the mechanical one is related to the stiffness of the tongue's body. The first model, in which the stiffness remains uncontrolled, is in agreement with the standard UCM hypothesis. In contrast, the second optimum internal model, in which the stiffness is prescribed, displays the good variability of speech (at least, in the reasonable range of stiffness) and is in agreement with the more recent versions of the uncontrolled manifold hypothesis (UCM). There is also a rich clinical literature on internal models including work from John Krakauer,^[8] Pietro Mazzoni, Maurice A. Smith, Kurt Thoroughman, Joern Diedrichsen, and Amy Bastian.

References