Hypersurface
- For differential geometry usage, see glossary of differential geometry and topology.
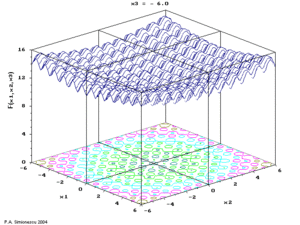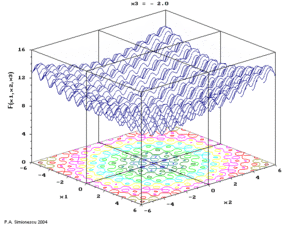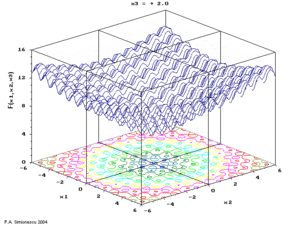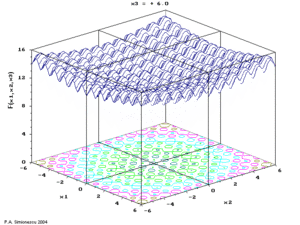
Ackley's function of three variables, with time the 3rd variable. | |
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface. Equivalently, the codimension of a hypersurface is one. For example, the n-sphere in Rn+1 is called a hypersphere. Hypersurfaces occur frequently in multivariable calculus as level sets.
In Rn, every closed hypersurface is orientable.[1] Every connected compact hypersurface is a level set,[2] and separates Rn in two connected components,[2] which is related to the Jordan–Brouwer separation theorem.
In algebraic geometry, a hypersurface in projective space of dimension n is an algebraic set (algebraic variety) that is purely of dimension n − 1. It is then defined by a single equation f(x1, x2, ..., xn) = 0, a homogeneous polynomial in the homogeneous coordinates.
Thus, it generalizes those algebraic curves f(x1, x2) = 0 (dimension one), and those algebraic surfaces f(x1, x2, x3) = 0 (dimension two), when they are defined by homogeneous polynomials.
A hypersurface may have singularities, and hence is not necessarily a submanifold in the strict sense. "Primal" is an old term for an irreducible hypersurface.
See also
References
- ↑ Hans Samelson (1969) Orientability of hypersurfaces in Rn, Proceedings of the American Mathematical Society 22(1): 301,2
- 1 2 Elon L. Lima, "The Jordan-Brouwer separation theorem for smooth hypersurfaces", The American Mathematical Monthly, Vol. 95, No. 1 (Jan., 1988), pp. 39–42.
- Hazewinkel, Michiel, ed. (2001), "Hypersurface", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Shoshichi Kobayashi and Katsumi Nomizu (1969), Foundations of Differential Geometry Vol II, Wiley Interscience
- P.A. Simionescu & D. Beal (2004) Visualization of hypersurfaces and multivariable (objective ) functions by partial globalization, The Visual Computer 20(10):665–81.