Grundy number

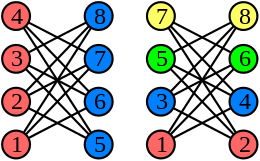
This article is about greedy coloring of graphs. For the system of arithmetic used in combinatorial game theory, see nimber. For the value of an impartial game, see Sprague–Grundy theorem.
An optimal greedy coloring (left) and Grundy coloring (right) of a crown graph. The numbers indicate the order in which the greedy algorithm colors the vertices.

In graph theory, the Grundy number or Grundy chromatic number of an undirected graph is the maximum number of colors that can be used by a greedy coloring strategy that considers the vertices of the graph in sequence and assigns each vertex its first available color, using a vertex ordering chosen to use as many colors as possible. Grundy numbers are named after P. M. Grundy, who studied an analogous concept for directed graphs in 1939.[1] The undirected version was introduced by Christen & Selkow (1979).[2]

Example

For example, for a path graph with four vertices, the chromatic number is two but the Grundy number is three: if the two endpoints of the path are colored first, the greedy coloring algorithm will use three colors for the whole graph.

Atoms

Zaker (2006) defines a sequence of graphs called t-atoms, with the property that a graph has Grundy number at least t if and only if it contains a t-atom. Each t-atom is formed from an independent set and a (t − 1)-atom, by adding one edge from each vertex of the (t − 1)-atom to a vertex of the independent set, in such a way that each member of the independent set has at least one edge incident to it. A Grundy coloring of a t-atom can be obtained by coloring the independent set first with the smallest-numbered color, and then coloring the remaining (t − 1)-atom with an additional t − 1 colors. For instance, the only 1-atom is a single vertex, and the only 2-atom is a single edge, but there are two possible 3-atoms: a triangle and a four-vertex path.[3]

In sparse graphs

For a graph with n vertices and degeneracy d, the Grundy number is O(d log n). In particular, for graphs of bounded degeneracy (such as planar graphs) or graphs for which the chromatic number and degeneracy are bounded within constant factors of each other (such as chordal graphs) the Grundy number and chromatic number are within a logarithmic factor of each other.[4] For interval graphs, the chromatic number and Grundy number are within a factor of 8 of each other.[5]

Computational complexity

Testing whether the Grundy number of a given graph is at least k, for a fixed constant k, can be performed in polynomial time, by searching for all possible k-atoms that might be subgraphs of the given graph. However, this algorithm is not fixed-parameter tractable, because the exponent in its running time depends on k. When k is an input variable rather than a parameter, the problem is NP-complete.[3] The Grundy number is at most one plus the maximum degree of the graph, and it remains NP-complete to test whether it equals one plus the maximum degree.[6] There exists a constant c > 1 such that it is NP-hard under randomized reductions to approximate the Grundy number to within an approximation ratio better than c.[7]

There is an exact exponential time algorithm for the Grundy number that runs in time O(2.443n).[8]

For trees, and graphs of bounded treewidth, the Grundy number may be unboundedly large.[9] Nevertheless, the Grundy number can be computed in polynomial time for trees, and is fixed-parameter tractable when parameterized by the treewidth,[10] although (assuming the exponential time hypothesis) the dependence on treewidth must be greater than singly exponential.[8] When parameterized by the Grundy number itself, it can be computed in fixed-parameter tractable time for chordal graphs and claw-free graphs,[8] and also (using general results on subgraph isomorphism in sparse graphs to search for atoms) for graphs of bounded expansion.[8][11][12]

Well-colored graphs

A graph is called well-colored if its Grundy number equals its chromatic number. Testing whether a graph is well-colored is coNP-complete.[3] The hereditarily well-colored graphs (graphs for which every induced subgraph is well-colored) are exactly the cographs, the graphs that do not have a four-vertex path as an induced subgraph.[2]

References

  1. ↑ Grundy, P. M. (1939), "Mathematics and games", Eureka, 2: 6–8. As cited by Erdős, Paul; Hedetniemi, Stephen T.; Laskar, Renu C.; Prins, Geert C. E. (2003), "On the equality of the partial Grundy and upper ochromatic numbers of graphs", Discrete Mathematics, 272 (1): 53–64, doi:10.1016/S0012-365X(03)00184-5, MR 2019200.
  2. 1 2 Christen, Claude A.; Selkow, Stanley M. (1979), "Some perfect coloring properties of graphs", Journal of Combinatorial Theory, Series B, 27 (1): 49–59, doi:10.1016/0095-8956(79)90067-4, MR 539075.
  3. 1 2 3 Zaker, Manouchehr (2006), "Results on the Grundy chromatic number of graphs", Discrete Mathematics, 306 (23): 3166–3173, doi:10.1016/j.disc.2005.06.044, MR 2273147.
  4. ↑ Irani, Sandy (1994), "Coloring inductive graphs on-line", Algorithmica, 11 (1): 53–72, doi:10.1007/BF01294263, MR 1247988.
  5. ↑ Narayanaswamy, N. S.; Subhash Babu, R. (2008), "A note on first-fit coloring of interval graphs", Order, 25 (1): 49–53, doi:10.1007/s11083-008-9076-6, MR 2395157.
  6. ↑ Havet, Frédéric; Sampaio, Leonardo (2010), "On the Grundy number of a graph", Parameterized and exact computation, Lecture Notes in Comput. Sci., 6478, Springer, Berlin, pp. 170–179, doi:10.1007/978-3-642-17493-3_17, MR 2770795.
  7. ↑ Kortsarz, Guy (2007), "A lower bound for approximating Grundy numbering", Discrete Mathematics & Theoretical Computer Science, 9 (1).
  8. 1 2 3 4 Bonnet, Édouard; Foucaud, Florent; Kim, Eun Jung; Sikora, Florian (2015), "Complexity of Grundy coloring and its variants", Computing and combinatorics, Lecture Notes in Comput. Sci., 9198, Springer, Cham, pp. 109–120, doi:10.1007/978-3-319-21398-9_9, MR 3447246.
  9. ↑ Gyárfás, A.; Lehel, J. (1988), "On-line and first fit colorings of graphs", Journal of Graph Theory, 12 (2): 217–227, doi:10.1002/jgt.3190120212, MR 940831.
  10. ↑ Telle, Jan Arne; Proskurowski, Andrzej (1997), "Algorithms for vertex partitioning problems on partial k-trees", SIAM Journal on Discrete Mathematics, 10 (4): 529–550, doi:10.1137/S0895480194275825, MR 1477655.
  11. ↑ Dvořák, Zdeněk; Kráľ, Daniel; Thomas, Robin (2010), "Deciding first-order properties for sparse graphs", Proc. 51st Annual IEEE Symposium on Foundations of Computer Science (FOCS 2010), IEEE Computer Soc., Los Alamitos, CA, pp. 133–142, MR 3024787.
  12. ↑ Nešetřil, Jaroslav; Ossona de Mendez, Patrice (2012), "18.3 The Subgraph Isomorphism Problem and Boolean Queries", Sparsity: Graphs, Structures, and Algorithms, Algorithms and Combinatorics, 28, Springer, pp. 400–401, doi:10.1007/978-3-642-27875-4, ISBN 978-3-642-27874-7, MR 2920058.
This article is issued from Wikipedia - version of the 11/21/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.