Glushkov's construction algorithm

In computer science theory – particularly formal language theory – the Glushkov Construction Algorithm (GCA) transforms a given regular expression into an equivalent nondeterministic finite automaton (NFA). Thus, it forms a bridge between regular expressions and nondeterministic finite automata: two abstract representations of formal languages.

The NFA format is better suited for execution on a computer when regular expressions are used. These expressions may be used to describe advanced search patterns in "find and replace"-like operations of text processing utilities. This algorithm can be considered a compiler from a regular expression to an NFA, which is why this algorithm is of practical interest. Furthermore, the automaton is small by nature, as the number of states is equal to the number of letters of the regular expression, plus one.

Thus, an automaton can be made deterministic by the powerset construction and then be minimized to get an optimal automaton corresponding to the given regular expression.

From another, more theoretical point of view, this algorithm is a part of the proof that they both accept exactly the same languages; that is, the regular languages. The converse of Glushkov's algorithm is Kleene's algorithm, which transforms a finite automaton into a regular expression. The automaton obtained by Glushkov's construction is the same as the one obtained by Thompson's construction algorithm, once their ε-transition is removed.

Construction

Given a regular expression $e$ , the Glushkov Construction Algorithm creates a non-deterministic automaton that accepts the language $L(e)$ accepted by $e$ .^[1] The construction uses four steps:

1. Linearisation of the expression. Each letter of the alphabet appearing in the expression is renamed, so that each letter occurs at most once in the new expression. Let $A$ be the old alphabet and let $B$ be the new one.

2a. Computation of the sets $P(e')$ , $D(e')$ , and $F(e')$ , where $e'$ is the linearity version of $e$ . The first, $P(e')$ , is the set of letters which occurs as first letter of a word of $L(e')$ . The second, $D(e')$ , is the set of letters which can ends a letter of $L(e')$ . The last one is the set of pairs of letters which can occur in words of $L(e')$ , which is the set of factors of length two of the words of $L(e')$ . Those sets are mathematically defined by

P(e')=\{a\in B\mid aB^*\cap L(e')\ne\emptyset\}

D(e')=\{a\in B\mid B^{*}a\cap L(e')\neq \emptyset \}

F(e')=\{u\in B^2\mid B^*uB^*\cap L(e')\ne\emptyset\}

They are computed by induction over the structure of the expression, as explained below, but they are a function of the language and not of the expression.

2b. Computation of the set $\Lambda(e')$ which contains the empty-word if this word belongs to $L(e')$ , and is the empty-set otherwise. Formally, this is $\Lambda(e')=\{\varepsilon\}\cap L(e')$ , where $\varepsilon$ is the empty-word.

3. Computation of the local language, as defined by $P(e')$ , $D(e')$ , $F(e')$ , and $\Lambda(e')$ . By definition, the local language defined by the sets $P$ , $D$ , and $F$ is the set of words which begin with a letter of $P$ , end by a letter of $D$ , and whose factors of length 2 belong to $F$ ; that is, it is the language:

L=(PA^*\cap A^*D)\setminus A^*(A^2\setminus F)A^*

potentially with the empty word.

The computation of the automaton for the local language denoted by this linearised expression is formally known as Glushkov's construction. The construction of the automaton can be done using classical construction operations: concatenation, intersection and itering an automaton.

4. Erasing the delineation, giving to each letter of $B$ the letter of $A$ it used to be.

Example

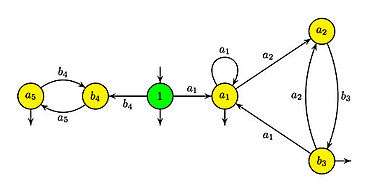
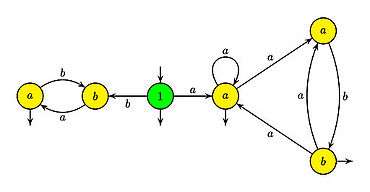
Automaton constructed by Glushkov's algorithm – linear version

Automaton constructed by Glushkov's algorithm - final version

Consider^[1] the rational expression $e = (a(ab)^*)^* + (ba)^*$ .

1. The linearized version is

e'=(a_1(a_2b_3)^*)^*+(b_4a_5)^*

The letters have been linearized by appending an index to them.

2. The sets $P$ , $D$ , and $F$ of the first letters, last letters, and factors of length 2 for the linear expression are respectively

$P(e')=\{a_1,b_4\}$ ,
$D(e')=\{a_1,b_3,a_5\}$ ,
$F(e')=\{a_1a_2, a_1a_1, a_2b_3, b_3a_1,b_3a_2,b_4a_5,a_5b_4\}$ .

The empty word belongs to the language, hence $\Lambda(e')=\{1\}$ .

3. The automaton of the local language

L'=P'B^*\cap B^*D'\setminus B^*(B^2\setminus F')B^*

contains an initial state, denoted 1, and a state for each of the five letters of the alphabet

B=\{a_1, a_2, b_3, b_4, a_5\}

There is a transition from 1 to the two states of $P'$ , a transition from $a$ to $b$ if $ab$ is in $F'$ , and the three states of $D'$ are final, and such is the state 1. All transitions to a letter $b$ have as label the letter $b$ .

4. Obtain the automaton for $L(e)$ by deleting the indices.

Computation of the set of letters

The computation of the sets $P$ , $D$ , $F$ , and $\Lambda$ is done inductively over the expression. One must give the values for 0, 1 (the symbols for the empty language and the singleton language containing the empty-word), the letters, and the results of the operations $+,\cdot,*$ .

1. For $\Lambda$ , one has

\Lambda (0)=\emptyset

\Lambda (1)=\{1\}

\Lambda(a)=\emptyset

for all letters $a$ , then

\Lambda(e+f)=\Lambda(e)\cup\Lambda(f), \Lambda(e\cdot f)=\Lambda(e)\cdot \Lambda(f)

and then $\Lambda(e^*)=\{1\}$

2. For $P$ , one has

P(0)=P(1)=\emptyset

and

P(a)=\{a\}

for each letter $a$ , then

P(e+f)=P(e)\cup P(f), P(e\cdot f)= P(e)\cup\Lambda(e)P(f)

and finally $P(e^*)=P(e)$ .

The same formulas are also correct for $D$ , apart from the product where

D(e\cdot f)= D(f)\cup D(e) \Lambda(f)

3. For the set of factors of length 2, one has

F(0)=F(1)=F(a)=\emptyset

for all letters $a$ , then

F(e+f)=F(e)\cup F(f),F(e\cdot f)=F(e)\cup F(f)\cup D(e)P(f)

and finally $F(e^{*})=F(e)\cup D(e)P(e)$ .

The most costly operations are the products of sets for the computation of $F$ .

Properties

The obtained automaton is non-deterministic, and it has as many states as the number of letters of the rational expression, plus one. Furthermore, it has been shown ^[2] that Glushkov's automaton is the same as Thompson's automaton when the ε-transitions are removed.

Applications and deterministic expressions

The computation of the automaton by the expression occurs often; it has been systematically used in search functions, in particular by the Unix grep command. Similarly, XML's specification also uses such constructions; for more efficiency, regular expressions of a certain kind, called deterministic expressions, have been studied.^[2]^[3]

Notes and references

1 2 (Pin 2010).
1 2 (Sakarovitch 2003, p. 215).
↑ Brüggemann-Klein, Anne (1993). "Regular Expressions into Finite Automata". Theoretical Computer Science. 12 (2): 197–213. doi:10.1016/0304-3975(93)90287-4. .

External links

A Unified Construction of the Glushkov, Follow, and Antimirov Automata

Algorithms and Computation: 14th International Symposium, ISAAC

This article is issued from Wikipedia - version of the 11/16/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.