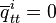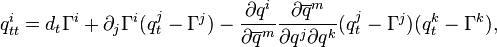Free motion equation

A free motion equation is a differential equation that describes a mechanical system in the absence of external forces, but in the presence only of an inertial force depending on the choice of a reference frame. In non-autonomous mechanics on a configuration space 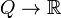Q\to \mathbb R, a free motion equation is defined as a second order non-autonomous dynamic equation on 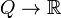Q\to \mathbb R which is brought into the form

\overline q^i_{tt}=0

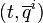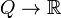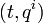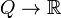with respect to some reference frame (t,\overline q^i) on Q\to \mathbb R. Given an arbitrary reference frame (t,q^i) on Q\to \mathbb R, a free motion equation reads

q^i_{tt}=d_t\Gamma^i +\partial_j\Gamma^i(q^j_t-\Gamma^j) - \frac{\partial q^i}{\partial\overline q^m}\frac{\partial\overline q^m}{\partial q^j\partial q^k}(q^j_t-\Gamma^j) (q^k_t-\Gamma^k),

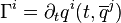where \Gamma^i=\partial_t q^i(t,\overline q^j) is a connection on 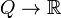Q\to \mathbb R associates with the initial reference frame 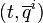(t,\overline q^i). The right-hand side of this equation is treated as an inertial force.

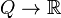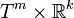A free motion equation need not exist in general. It can be defined if and only if a configuration bundle Q\to\mathbb R of a mechanical system is a toroidal cylinder T^m\times \mathbb R^k.

References

See also

This article is issued from Wikipedia - version of the 7/1/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.