Flower snark
| Flower snark | |
|---|---|
|
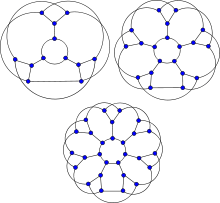
The flower snarks J3, J5 and J7. | |
| Vertices | 4n |
| Edges | 6n |
| Girth |
3 for n=3 5 for n=5 6 for n≥7 |
| Chromatic number | 3 |
| Chromatic index | 4 |
| Properties | Snark for n≥5 |
| Notation | Jn with n odd |
| Flower snark J5 | |
|---|---|
|
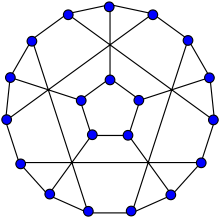
The flower snark J5. | |
| Vertices | 20 |
| Edges | 30 |
| Girth | 5 |
| Chromatic number | 3 |
| Chromatic index | 4 |
| Properties |
Snark Hypohamiltonian |
In the mathematical field of graph theory, the flower snarks form an infinite family of snarks introduced by Rufus Isaacs in 1975.[1]
As snarks, the flower snarks are connected, bridgeless cubic graphs with chromatic index equal to 4. The flower snarks are non-planar and non-hamiltonian.
Construction
The flower snark Jn can be constructed with the following process :
- Build n copies of the star graph on 4 vertices. Denote the central vertex of each star Ai and the outer vertices Bi, Ci and Di. This results in a disconnected graph on 4n vertices with 3n edges (Ai-Bi, Ai-Ci and Ai-Di for 1≤i≤n).
- Construct the n-cycle (B1... Bn). This adds n edges.
- Finally construct the 2n-cycle (C1... CnD1... Dn). This adds 2n edges.
By construction, the Flower snark Jn is a cubic graph with 4n vertices and 6n edges. For it to have the required properties, n should be odd.
Special cases
The name flower snark is sometimes used for J5, a flower snark with 20 vertices and 30 edges.[2] It is one of 6 snarks on 20 vertices (sequence A130315 in the OEIS). The flower snark J5 is hypohamiltonian.[3]
J3 is a trivial variation of the Petersen graph formed by replacing one of its vertices by a triangle. This graph is also known as the Tietze's graph.[4] In order to avoid trivial cases, snarks are generally restricted to have girth at least 5. With that restriction, J3 is not a snark.
Gallery
-
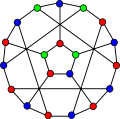
The chromatic number of the flower snark J5 is 3.
-
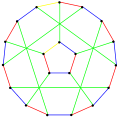
The chromatic index of the flower snark J5 is 4.
-
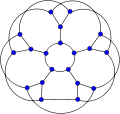
The original representation of the flower snark J5.
References
- ↑ Isaacs, R. "Infinite Families of Nontrivial Trivalent Graphs Which Are Not Tait Colorable." Amer. Math. Monthly 82, 221–239, 1975.
- ↑ Weisstein, Eric W. "Flower Snark". MathWorld.
- ↑ Weisstein, Eric W. "Hypohamiltonian Graph". MathWorld.
- ↑ Clark, L.; Entringer, R. (1983), "Smallest maximally nonhamiltonian graphs", Periodica Mathematica Hungarica, 14 (1): 57–68, doi:10.1007/BF02023582.