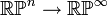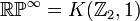Essential manifold
Essential manifold a special type of closed manifolds. The notion was first introduced explicitly by Mikhail Gromov.[1]
Definition
A closed manifold M is called essential if its fundamental class [M] defines a nonzero element in the homology of its fundamental group π, or more precisely in the homology of the corresponding Eilenberg–MacLane space K(π, 1), via the natural homomorphism
,
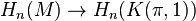where n is the dimension of M. Here the fundamental class is taken in homology with integer coefficients if the manifold is orientable, and in coefficients modulo 2, otherwise.
Examples
- All closed surfaces (i.e. 2-dimensional manifolds) are essential with the exception of the 2-sphere S2.
- Real projective space RPn is essential since the inclusion
- is injective in homology, where
- is the Eilenberg–MacLane space of the finite cyclic group of order 2.
- All compact aspherical manifolds are essential (since being aspherical means the manifold itself is already a K(π, 1))
- In particular all compact hyperbolic manifolds are essential.
- All lens spaces are essential.
Properties
- The connected sum of essential manifolds is essential.
- Any manifold which admits a map of nonzero degree to an essential manifold is itself essential.
References
- ↑ Gromov, M.: Filling Riemannian manifolds, J. Diff. Geom. 18 (1983), 1–147.
See also
| ||||||||||||||
This article is issued from Wikipedia - version of the 10/6/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.