Dwadasama

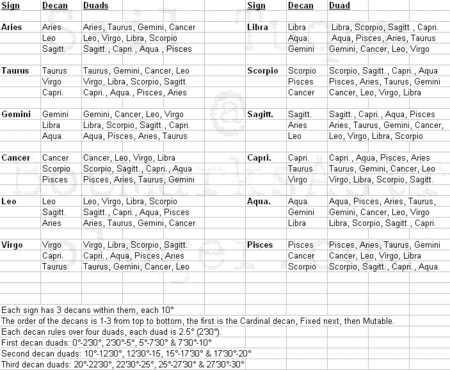
In astrology, a dwadasamsa, which is also called a dwad, duad or dwadachamsha, is 1/12 of a zodiacal sign. The dwadasama was developed by Hindu astrologers who broke the 30 degree sign down into 12 equal parts of 2.5 degrees each. It is based upon the principle of the part being a reflection of the whole, and 12 signs of the zodiac were placed within the confines of one sign. It is believed that these signs within a sign, by virtue of their planetary rulers, account for subtle shadings of expression found in different degrees of that sign. Therefore, in addition to the sign having a primary planetary ruler, it would also have a sub-ruler, based upon which dwadasama it is placed in.

For example, if an individual's Sun is placed in 10 degrees 51 minutes Aquarius then their Sun sign would be ruled by Uranus, but the dwad, being in the range of 10 to 12.5 degrees would be placed within Gemini(the 5th dwad), so the individual's sub-ruler would be the Mercury, which rules Gemini.

A listing of the dwads for each sign is found in the diagram below:

1 2 3 4 5 6 7 8 9 10 11 12
Ar Ar Ta Ge Ca Le Vi Li Sc Sa Cp Aq Pi
Ta Ta Ge Ca Le Vi Li Sc Sa Cp Aq Pi Ar
Ge Ge Ca Le Vi Li Sc Sa Cp Aq Pi Ar Ta
Ca Ca Le Vi Li Sc Sa Cp Aq Pi Ar Ta Ge
Le Le Vi Li Sc Sa Cp Aq Pi Ar Ta Ge Ca
Vi Vi Li Sc Sa Cp Aq Pi Ar Ta Ge Ca Le
Li Li Sc Sa Cp Aq Pi Ar Ta Ge Ca Le Vi
Sc Sc Sa Cp Aq Pi Ar Ta Ge Ca Le Vi Li
Sa Sa Cp Aq Pi Ar Ta Ge Ca Le Vi Li Sc
Cp Cp Aq Pi Ar Ta Ge Ca Le Vi Li Sc Sa
Aq Aq Pi Ar Ta Ge Ca Le Vi Li Sc Sa Cp
Pi Pi Ar Ta Ge Ca Le Vi Li Sc Sa Cp Aq

Decanates & Duads

Here, we see two ways of dividing the astrological signs combined, first the ten degrees decans, then the 2.5 degree duads:

References

    This article is issued from Wikipedia - version of the 11/28/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.