Distorted Schwarzschild metric
The distorted Schwarzschild metric refers to the metric of a standard/isolated Schwarzschild spacetime exposed in external fields. In numerical simulation, the Schwarzschild metric can be distorted by almost arbitrary kinds of external energy–momentum distribution. However, in exact analysis, the mature method to distort the standard Schwarzschild metric is restricted to the framework of Weyl metrics.
Standard Schwarzschild as a vacuum Weyl metric
All static axisymmetric solutions of the Einstein-Maxwell equations can be written in the form of Weyl's metric,[1]
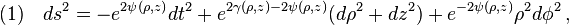
From the Weyl perspective, the metric potentials generating the standard Schwarzschild solution are given by[1][2]
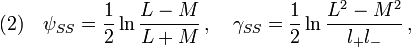
where
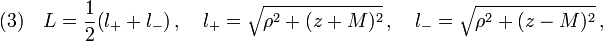
which yields the Schwarzschild metric in Weyl's canonical coordinates that
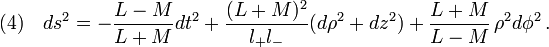
Weyl-distortion of Schwarzschild's metric
Vacuum Weyl spacetimes (such as Schwarzschild) respect the following field equations,[1][2]
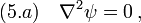
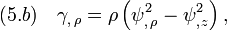
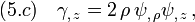
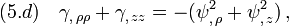
where 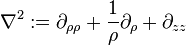 is the Laplace operator.
is the Laplace operator.
The vacuum Einstein's equation reads 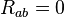 , which yields Eqs(5.a)-(5.c).
, which yields Eqs(5.a)-(5.c).
Moreover, the supplementary relation 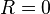 implies Eq(5.d).
implies Eq(5.d).
Eq(5.a) is the linear Laplace's equation; that is to say, linear combinations of given solutions are still its solutions. Given two solutions 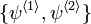 to Eq(5.a), one can construct a new solution via
to Eq(5.a), one can construct a new solution via
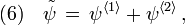
and the other metric potential can be obtained by
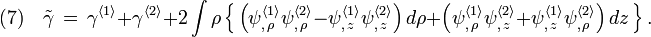
Let  and
and  , while
, while 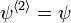 and
and 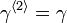 refer to a second set of Weyl metric potentials. Then,
refer to a second set of Weyl metric potentials. Then, 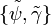 constructed via
Eqs(6)(7) leads to the superposed Schwarzschild-Weyl metric
constructed via
Eqs(6)(7) leads to the superposed Schwarzschild-Weyl metric
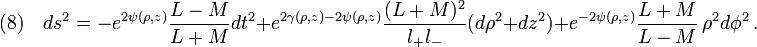
With the transformations[2]
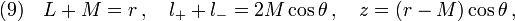
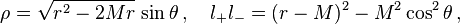
one can obtain the superposed Schwarzschild metric in the usual 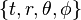 coordinates,
coordinates,
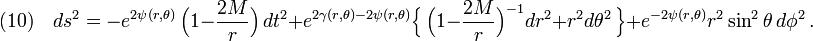
The superposed metric Eq(10) can be regarded as the standard Schwarzschild metric distorted by external Weyl sources. In the absence of distortion potential 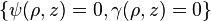 , Eq(10) reduces to the standard Schwarzschild metric
, Eq(10) reduces to the standard Schwarzschild metric
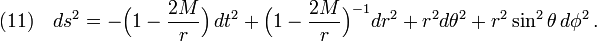
Weyl-distorted Schwarzschild solution in spherical coordinates
Similar to the exact vacuum solutions to Weyl's metric in spherical coordinates, we also have series solutions to Eq(10). The distortion potential 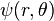 in Eq(10) is given by the multipole expansion[3]
in Eq(10) is given by the multipole expansion[3]
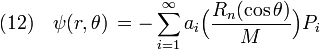 with
with ![R:=\Big[\Big(1-\frac{2M}{r} \Big) r^2 +M^2\cos^2\theta \Big]^{1/2}](../I/m/9ed68d9a8ab934054ca23517fd55c231.png)
where
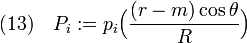
denotes the Legendre polynomials and 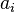 are multipole coefficients. The other potential
are multipole coefficients. The other potential 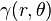 is
is
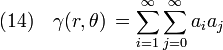
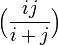
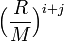
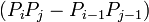
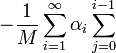
![\Big[(-1)^{i+j}(r-M(1-\cos\theta))+r-M(1+\cos\theta) \Big]](../I/m/56a5ae49b54795264c932d8ddb654aa8.png)
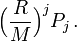
See also
References
- 1 2 3 Jeremy Bransom Griffiths, Jiri Podolsky. Exact Space-Times in Einstein's General Relativity. Cambridge: Cambridge University Press, 2009. Chapter 10.
- 1 2 3 R Gautreau, R B Hoffman, A Armenti. Static multiparticle systems in general relativity. IL NUOVO CIMENTO B, 1972, 7(1): 71-98.
- ↑ Terry Pilkington, Alexandre Melanson, Joseph Fitzgerald, Ivan Booth. "Trapped and marginally trapped surfaces in Weyl-distorted Schwarzschild solutions". Classical and Quantum Gravity, 2011, 28(12): 125018. arXiv:1102.0999v2[gr-qc]