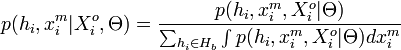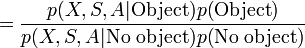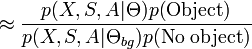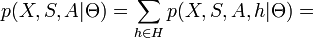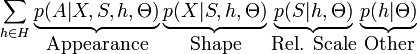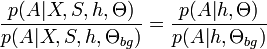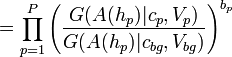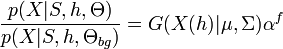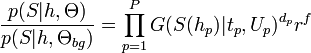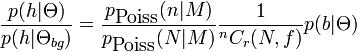Constellation model
The constellation model is a probabilistic, generative model for category-level object recognition in computer vision. Like other part-based models, the constellation model attempts to represent an object class by a set of N parts under mutual geometric constraints. Because it considers the geometric relationship between different parts, the constellation model differs significantly from appearance-only, or "bag-of-words" representation models, which explicitly disregard the location of image features.
The problem of defining a generative model for object recognition is difficult. The task becomes significantly complicated by factors such as background clutter, occlusion, and variations in viewpoint, illumination, and scale. Ideally, we would like the particular representation we choose to be robust to as many of these factors as possible.
In category-level recognition, the problem is even more challenging because of the fundamental problem of intra-class variation. Even if two objects belong to the same visual category, their appearances may be significantly different. However, for structured objects such as cars, bicycles, and people, separate instances of objects from the same category are subject to similar geometric constraints. For this reason, particular parts of an object such as the headlights or tires of a car still have consistent appearances and relative positions. The Constellation Model takes advantage of this fact by explicitly modeling the relative location, relative scale, and appearance of these parts for a particular object category. Model parameters are estimated using an unsupervised learning algorithm, meaning that the visual concept of an object class can be extracted from an unlabeled set of training images, even if that set contains "junk" images or instances of objects from multiple categories. It can also account for the absence of model parts due to appearance variability, occlusion, clutter, or detector error.
History
The idea for a "parts and structure" model was originally introduced by Fischler and Elschlager in 1973.[1] This model has since been built upon and extended in many directions. The Constellation Model, as introduced by Dr. Perona and his colleagues, was a probabilistic adaptation of this approach.
In the late '90s, Burl et al.[2][3][4][5] revisited the Fischler and Elschlager model for the purpose of face recognition. In their work, Burl et al. used manual selection of constellation parts in training images to construct a statistical model for a set of detectors and the relative locations at which they should be applied. In 2000, Weber et al. [6][7][8][9] made the significant step of training the model using a more unsupervised learning process, which precluded the necessity for tedious hand-labeling of parts. Their algorithm was particularly remarkable because it performed well even on cluttered and occluded image data. Fergus et al.[10][11] then improved upon this model by making the learning step fully unsupervised, having both shape and appearance learned simultaneously, and accounting explicitly for the relative scale of parts.
The method of Weber and Welling et al.[9]
In the first step, a standard interest point detection method, such as Harris corner detection, is used to generate interest points. Image features generated from the vicinity of these points are then clustered using k-means or another appropriate algorithm. In this process of vector quantization, one can think of the centroids of these clusters as being representative of the appearance of distinctive object parts. Appropriate feature detectors are then trained using these clusters, which can be used to obtain a set of candidate parts from images.
As a result of this process, each image can now be represented as a set of parts. Each part has a type, corresponding to one of the aforementioned appearance clusters, as well as a location in the image space.
Basic generative model
Weber & Welling here introduce the concept of foreground and background. Foreground parts correspond to an instance of a target object class, whereas background parts correspond to background clutter or false detections.
Let T be the number of different types of parts. The positions of all parts extracted from an image can then be represented in the following "matrix,"
where 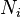 represents the number of parts of type
represents the number of parts of type 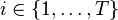 observed in the image. The superscript o indicates that these positions are observable, as opposed to missing. The positions of unobserved object parts can be represented by the vector
observed in the image. The superscript o indicates that these positions are observable, as opposed to missing. The positions of unobserved object parts can be represented by the vector 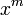 . Suppose that the object will be composed of
. Suppose that the object will be composed of 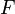 distinct foreground parts. For notational simplicity, we assume here that
distinct foreground parts. For notational simplicity, we assume here that 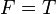 , though the model can be generalized to
, though the model can be generalized to 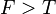 . A hypothesis
. A hypothesis 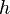 is then defined as a set of indices, with
is then defined as a set of indices, with 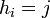 , indicating that point
, indicating that point 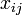 is a foreground point in
is a foreground point in 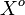 . The generative probabilistic model is defined through the joint probability density
. The generative probabilistic model is defined through the joint probability density 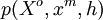 .
.
Model details
The rest of this section summarizes the details of Weber & Welling's model for a single component model. The formulas for multiple component models[8] are extensions of those described here.
To parametrize the joint probability density, Weber & Welling introduce the auxiliary variables 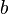 and
and 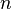 , where
, where 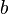 is a binary vector encoding the presence/absence of parts in detection (
is a binary vector encoding the presence/absence of parts in detection (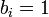 if
if 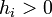 , otherwise
, otherwise 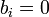 ), and
), and 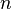 is a vector where
is a vector where 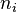 denotes the number of background candidates included in the
denotes the number of background candidates included in the 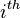 row of
row of 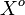 . Since
. Since 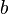 and
and 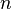 are completely determined by
are completely determined by 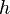 and the size of
and the size of 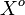 , we have
, we have 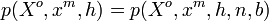 . By decomposition,
. By decomposition,
The probability density over the number of background detections can be modeled by a Poisson distribution,
where 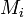 is the average number of background detections of type
is the average number of background detections of type 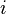 per image.
per image.
Depending on the number of parts 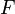 , the probability
, the probability 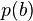 can be modeled either as an explicit table of length
can be modeled either as an explicit table of length 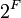 , or, if
, or, if 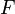 is large, as
is large, as 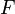 independent probabilities, each governing the presence of an individual part.
independent probabilities, each governing the presence of an individual part.
The density 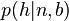 is modeled by
is modeled by
where 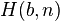 denotes the set of all hypotheses consistent with
denotes the set of all hypotheses consistent with 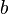 and
and 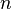 , and
, and 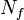 denotes the total number of detections of parts of type
denotes the total number of detections of parts of type 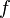 . This expresses the fact that all consistent hypotheses, of which there are
. This expresses the fact that all consistent hypotheses, of which there are 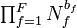 , are equally likely in the absence of information on part locations.
, are equally likely in the absence of information on part locations.
And finally,
where 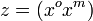 are the coordinates of all foreground detections, observed and missing, and
are the coordinates of all foreground detections, observed and missing, and 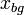 represents the coordinates of the background detections. Note that foreground detections are assumed to be independent of the background.
represents the coordinates of the background detections. Note that foreground detections are assumed to be independent of the background. 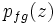 is modeled as a joint Gaussian with mean
is modeled as a joint Gaussian with mean 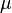 and covariance
and covariance 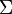 .
.
Classification
The ultimate objective of this model is to classify images into classes "object present" (class 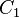 ) and "object absent" (class
) and "object absent" (class 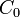 ) given the observation
) given the observation 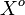 . To accomplish this, Weber & Welling run part detectors from the learning step exhaustively over the image, examining different combinations of detections. If occlusion is considered, then combinations with missing detections are also permitted. The goal is then to select the class with maximum a posteriori probability, by considering the ratio
. To accomplish this, Weber & Welling run part detectors from the learning step exhaustively over the image, examining different combinations of detections. If occlusion is considered, then combinations with missing detections are also permitted. The goal is then to select the class with maximum a posteriori probability, by considering the ratio
where 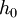 denotes the null hypothesis, which explains all parts as background noise. In the numerator, the sum includes all hypotheses, including the null hypothesis, whereas in the denominator, the only hypothesis consistent with the absence of an object is the null hypothesis. In practice, some threshold can be defined such that, if the ratio exceeds that threshold, we then consider an instance of an object to be detected.
denotes the null hypothesis, which explains all parts as background noise. In the numerator, the sum includes all hypotheses, including the null hypothesis, whereas in the denominator, the only hypothesis consistent with the absence of an object is the null hypothesis. In practice, some threshold can be defined such that, if the ratio exceeds that threshold, we then consider an instance of an object to be detected.
Model learning
After the preliminary step of interest point detection, feature generation and clustering, we have a large set of candidate parts over the training images. To learn the model, Weber & Welling first perform a greedy search over possible model configurations, or equivalently, over potential subsets of the candidate parts. This is done in an iterative fashion, starting with random selection. At subsequent iterations, parts in the model are randomly substituted, the model parameters are estimated, and the performance is assessed. The process is complete when further model performance improvements are no longer possible.
At each iteration, the model parameters
are estimated using expectation maximization. 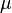 and
and 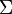 , we recall, are the mean and covariance of the joint Gaussian
, we recall, are the mean and covariance of the joint Gaussian 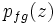 ,
, 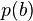 is the probability distribution governing the binary presence/absence of parts, and
is the probability distribution governing the binary presence/absence of parts, and 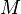 is the mean number of background detections over part types.
is the mean number of background detections over part types.
M-step
EM proceeds by maximizing the likelihood of the observed data,
with respect to the model parameters 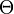 . Since this is difficult to achieve analytically, EM iteratively maximizes a sequence of cost functions,
. Since this is difficult to achieve analytically, EM iteratively maximizes a sequence of cost functions,
Taking the derivative of this with respect to the parameters and equating to zero produces the update rules:
E-step
The update rules in the M-step are expressed in terms of sufficient statistics, ![E[z]\,](../I/m/b9d0f77e58d861485dbc7a9b8abc41dc.png) ,
, ![E[zz^T]\,](../I/m/3ac8fa4de1d7d9e755c36b686d43e959.png) ,
, ![E[\delta_{b,\bar{b}}]\,](../I/m/6ff443d5794a69ae9edda56e2589f422.png) and
and ![E[n]\,](../I/m/cb9cd07c057929e469100a007256a15b.png) , which are calculated in the E-step by considering the posterior density:
, which are calculated in the E-step by considering the posterior density:
The method of Fergus et al.[10]
In Weber et al., shape and appearance models are constructed separately. Once the set of candidate parts had been selected, shape is learned independently of appearance. The innovation of Fergus et al. is to learn not only two, but three model parameters simultaneously: shape, appearance, and relative scale. Each of these parameters are represented by Gaussian densities.
Feature representation
Whereas the preliminary step in the Weber et al. method is to search for the locations of interest points, Fergus et al. use the detector of Kadir and Brady[12] to find salient regions in the image over both location (center) and scale (radius). Thus, in addition to location information 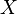 this method also extracts associated scale information
this method also extracts associated scale information 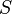 . Fergus et al. then normalize the squares bounding these circular regions to 11 x 11 pixel patches, or equivalently, 121-dimensional vectors in the appearance space. These are then reduced to 10-15 dimensions by principal component analysis, giving the appearance information
. Fergus et al. then normalize the squares bounding these circular regions to 11 x 11 pixel patches, or equivalently, 121-dimensional vectors in the appearance space. These are then reduced to 10-15 dimensions by principal component analysis, giving the appearance information 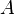 .
.
Model structure
Given a particular object class model with parameters 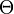 , we must decide whether or not a new image contains an instance of that class. This is accomplished by making a Bayesian decision,
, we must decide whether or not a new image contains an instance of that class. This is accomplished by making a Bayesian decision,
where 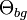 is the background model. This ratio is compared to a threshold
is the background model. This ratio is compared to a threshold 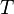 to determine object presence/absence.
to determine object presence/absence.
The likelihoods are factored as follows:
Appearance
Each part 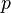 has an appearance modeled by a Gaussian density in the appearance space, with mean and covariance parameters
has an appearance modeled by a Gaussian density in the appearance space, with mean and covariance parameters 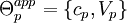 , independent of other parts' densities. The background model has parameters
, independent of other parts' densities. The background model has parameters 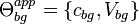 . Fergus et al. assume that, given detected features, the position and appearance of those features are independent. Thus,
. Fergus et al. assume that, given detected features, the position and appearance of those features are independent. Thus, 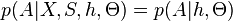 . The ratio of the appearance terms reduces to
. The ratio of the appearance terms reduces to
Recall from Weber et al. that 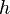 is the hypothesis for the indices of foreground parts, and
is the hypothesis for the indices of foreground parts, and 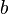 is the binary vector giving the occlusion state of each part in the hypothesis.
is the binary vector giving the occlusion state of each part in the hypothesis.
Shape
Shape is represented by a joint Gaussian density of part locations within a particular hypothesis, after those parts have been transformed into a scale-invariant space. This transformation precludes the need to perform an exhaustive search over scale. The Gaussian density has parameters 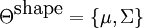 . The background model
. The background model 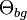 is assumed to be a uniform distribution over the image, which has area
is assumed to be a uniform distribution over the image, which has area 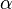 . Letting
. Letting 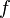 be the number of foreground parts,
be the number of foreground parts,
Relative scale
The scale of each part 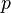 relative to a reference frame is modeled by a Gaussian density with parameters
relative to a reference frame is modeled by a Gaussian density with parameters 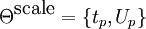 . Each part is assumed to be independent of other parts. The background model
. Each part is assumed to be independent of other parts. The background model 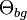 assumes a uniform distribution over scale, within a range
assumes a uniform distribution over scale, within a range  .
.
Occlusion and statistics of feature detection
The first factor models the number of features detected using a Poisson distribution, which has mean M. The second factor serves as a "book-keeping" factor for the hypothesis variable. The last factor is a probability table for all possible occlusion patterns.
Learning
The task of learning the model parameters 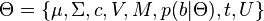 is accomplished by expectation maximization. This is carried out in a spirit similar to that of Weber et al. Details and formulas for the E-step and M-step can be seen in the literature.[11]
is accomplished by expectation maximization. This is carried out in a spirit similar to that of Weber et al. Details and formulas for the E-step and M-step can be seen in the literature.[11]
Performance
The Constellation Model as conceived by Fergus et al. achieves successful categorization rates consistently above 90% on large datasets of motorbikes, faces, airplanes, and spotted cats.[13] For each of these datasets, the Constellation Model is able to capture the "essence" of the object class in terms of appearance and/or shape. For example, face and motorbike datasets generate very tight shape models because objects in those categories have very well-defined structure, whereas spotted cats vary significantly in pose, but have a very distinctive spotted appearance. Thus, the model succeeds in both cases. It is important to note that the Constellation Model does not generally account for significant changes in orientation. Thus, if the model is trained on images of horizontal airplanes, it will not perform well on, for instance, images of vertically oriented planes unless the model is extended to account for this sort of rotation explicitly.
In terms of computational complexity, the Constellation Model is very expensive. If 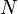 is the number of feature detections in the image, and
is the number of feature detections in the image, and 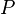 the number of parts in the object model, then the hypothesis space
the number of parts in the object model, then the hypothesis space 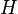 is
is 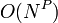 . Because the computation of sufficient statistics in the E-step of expectation maximization necessitates evaluating the likelihood for every hypothesis, learning becomes a major bottleneck operation. For this reason, only values of
. Because the computation of sufficient statistics in the E-step of expectation maximization necessitates evaluating the likelihood for every hypothesis, learning becomes a major bottleneck operation. For this reason, only values of 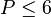 have been used in practical applications, and the number of feature detections
have been used in practical applications, and the number of feature detections 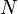 is usually kept within the range of about 20-30 per image.
is usually kept within the range of about 20-30 per image.
Variations
One variation that attempts to reduce complexity is the star model proposed by Fergus et al.[14] The reduced dependencies of this model allows for learning in 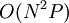 time instead of
time instead of 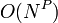 . This allows for a greater number of model parts and image features to be used in training. Because the star model has fewer parameters, it is also better at avoiding the problem of over-fitting when trained on fewer images.
. This allows for a greater number of model parts and image features to be used in training. Because the star model has fewer parameters, it is also better at avoiding the problem of over-fitting when trained on fewer images.
References
- ↑ M. Fischler and R. Elschlager. The Representation and Matching of Pictoral Structures. (1973)
- ↑ M. Burl, T. Leung, and P. Perona. Face Localization via Shape Statistics. (1995)
- ↑ T. Leung, M. Burl, and P. Perona. Finding Faces in Cluttered Scenes Using Random Labeled Graph Matching. (1995)
- ↑ M. Burl and P. Perona. Recognition of Planar Object Classes (1996)
- ↑ M. Burl, M. Weber, and P. Perona. A Probabilistic Approach to Object Recognition Using Local Photometry and Global Geometry (1998)
- ↑ M. Weber. Unsupervised Learning of Models for Object Recognition. PhD Thesis. (2000)
- ↑ M. Weber, W. Einhaeuser, M. Welling and P. Perona. Viewpoint-Invariant Learning and Detection of Human Heads. (2000)
- 1 2 M. Weber, M. Welling, and P. Perona. Towards Automatic Discovery of Object Categories. (2000)
- 1 2 M. Weber, M. Welling and P. Perona. Unsupervised Learning of Models for Recognition. (2000)
- 1 2 R. Fergus, P. Perona, and A. Zisserman. Object Class Recognition by Unsupervised Scale-Invariant Learning. (2003)
- 1 2 R. Fergus. Visual Object Category Recognition. PhD Thesis. (2005)
- ↑ T. Kadir and M. Brady. Saliency, scale and image description. (2001)
- ↑ R. Fergus and P. Perona. Caltech Object Category datasets. http://www.vision.caltech.edu/html-files/archive.html (2003)
- ↑ R. Fergus, P. Perona, and A. Zisserman. A Sparse Object Category Model for Efficient Learning and Exhaustive Recognition. (2005)
External links
- L. Fei-fei. Object categorization: the constellation models. Lecture Slides. (2005) (link not working)
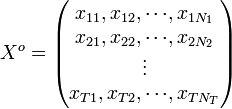
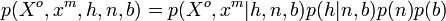
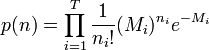
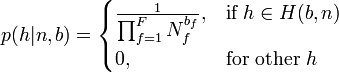
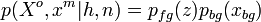
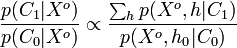
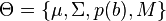
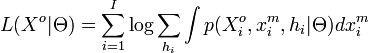
![Q(\tilde{\Theta}|\Theta) = \sum_{i=1}^I E[\log p(X_i^o,x_i^m,h_i|\tilde{\Theta})]](../I/m/b2c1660883050fe1bbade9426da9ebaf.png)
![\tilde{\mu} = \frac{1}{I} \sum_{i=1}^I E[z_i]](../I/m/4062c90b813671ac9beafdaf42d5299f.png)
![\tilde{\Sigma} = \frac{1}{I} \sum_{i=1}^I E[z_iz_i^T] - \tilde{\mu}\tilde{\mu}^T](../I/m/902fb58678eaaae5a36daf5869d7c84a.png)
![\tilde{p}(\bar{b}) = \frac{1}{I} \sum_{i=1}^I E[\delta_{b,\bar{b}}]](../I/m/f274e8bd7b6c2ba514053155b93f19cf.png)
![\tilde{M} = \frac{1}{I} \sum_{i=1}^I E[n_i]](../I/m/74bc1ec0852a86bca44104eca86b295c.png)