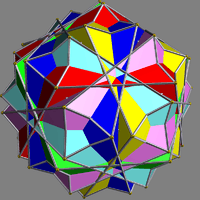
Compound of six pentagonal antiprisms

Compound of six pentagonal antiprisms
Type	Uniform compound
Index	UC27
Polyhedra	6 pentagonal antiprisms
Faces	60 triangles, 12 pentagons
Edges	120
Vertices	60
Symmetry group	icosahedral (Ih)
Subgroup restricting to one constituent	5-fold antiprismatic (D5d)

This uniform polyhedron compound is a symmetric arrangement of 6 pentagonal antiprisms. It can be constructed by inscribing within an icosahedron one pentagonal antiprism in each of the six possible ways, and then rotating each by 36 degrees about its axis (that passes through the centres of the two opposite pentagonal faces).

It shares its vertex arrangement with the compound of 6 pentagrammic crossed antiprisms.

Cartesian coordinates

Cartesian coordinates for the vertices of this compound are all the cyclic permutations of

(±(3+4τ), 0, ±(4−3τ))

(±(2−4τ), ±5τ, ±(1−2τ))

(±(2+τ), ±5, ±(4+2τ))

where τ = (1+√5)/2 is the golden ratio (sometimes written φ).

References

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79: 447–457, doi:10.1017/S0305004100052440, MR 0397554 .