Codazzi tensor

Codazzi tensors (named after Delfino Codazzi) arise very naturally in the study of Riemannian manifolds with harmonic curvature or harmonic Weyl tensor. In fact, existence of Codazzi tensors impose strict conditions on the curvature tensor of the manifold.

Definition

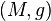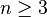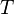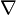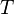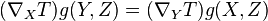Let $(M,g)$ be a n-dimensional Riemannian manifold for $n \geq 3$ , let $T$ be a tensor, and let $\nabla$ be a Levi-Civita connection on the manifold. We say that the tensor $T$ is a Codazzi Tensor if $(\nabla_X T) g(Y,Z) = (\nabla_Y T) g(X,Z)$ .

References

Arthur Besse, Einstein Manifolds, Springer (1987).

This article is issued from Wikipedia - version of the 7/10/2015. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Codazzi tensor

Definition

See also

References