Block-stacking problem
In statics, the block-stacking problem (also the book-stacking problem, or a number of other similar terms) is a puzzle concerning the stacking of blocks at the edge of a table.
Statement
The block-stacking problem is the following puzzle:
Place rigid rectangular blocks in a stable stack on a table edge in such a way as to maximize the overhang.
History
Paterson et al. provide a long list of references on this problem going back to mechanics texts from the middle of the 19th century.
Variants
Single-wide
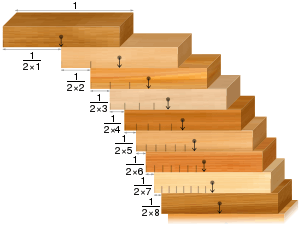
The single-wide problem involves having only one block at any given level. In the ideal case of perfectly rectangular blocks, the solution to the single-wide problem is that the maximum overhang is given by times the width of a block. This sum is one half of the corresponding partial sum of the harmonic series. Because the harmonic series diverges, the maximal overhang tends to infinity as increases, meaning that it is possible to achieve any arbitrarily large overhang, with sufficient blocks.
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Multi-wide
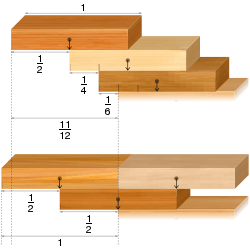
Multi-wide stacks using counterbalancing can give larger overhangs than a single width stack. Even for three blocks, stacking two counterbalanced blocks on top of another block can give an overhang of 1, while the overhang in the simple ideal case is at most 11/12. As Paterson et al. (2007) showed, asymptotically, the maximum overhang that can be achieved by multi-wide stacks is proportional to the cube root of the number of blocks, in contrast to the single-wide case in which the overhang is proportional to the logarithm of the number of blocks.
Robustness
Hall (2005) discusses this problem, shows that it is robust to nonidealizations such as rounded block corners and finite precision of block placing, and introduces several variants including nonzero friction forces between adjacent blocks.
References
- Hall, J. F. (2005). "Fun with stacking blocks". American Journal of Physics. 73 (12): 1107–1116. doi:10.1119/1.2074007.
- Paterson, Mike; Peres, Yuval; Thorup, Mikkel; Winkler, Peter; Zwick, Uri (2007). "Maximum overhang". arXiv:0707.0093
 [math.HO]..
[math.HO]..