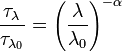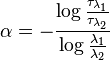Angstrom exponent

Ångström exponent is the name of the exponent in the formula that is usually used to describe the dependency of the aerosol optical thickness, or aerosol extinction coefficient on wavelength.

Depending on particle size distribution, the spectral dependence of the aerosol optical thickness is given approximately by

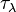\frac{\tau_\lambda}{\tau_{\lambda_0}}=\left (\frac{\lambda}{\lambda_0}\right )^{-\alpha}

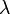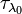where $\tau_\lambda$ is the optical thickness at wavelength $\lambda$ , and $\tau_{\lambda_0}$ is the optical thickness at the reference wavelength 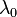$\lambda_0$ . In principle, if the optical thickness at one wavelength and the Ångström exponent are known, the optical thickness can be computed at a different wavelength. In practice, measurements are made of the optical thickness of an aerosol layer at two different wavelengths, and the Ångström exponent is estimated from these measurements using this formula. The aerosol optical thickness can then be derived at all other wavelengths, within the range of validity of this formula.

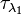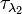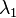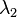For measurements of optical thickness $\tau_{\lambda_1}\,$ and $\tau_{\lambda_2}\,$ taken at two different wavelengths $\lambda_1\,$ and $\lambda_2\,$ respectively, the Ångström exponent is given by

\alpha = - \frac{\log \frac{\tau_{\lambda_1}}{\tau_{\lambda_2}}}{\log \frac{\lambda_1}{\lambda_2}}\,

The Ångström exponent is inversely related to the average size of the particles in the aerosol: the smaller the particles, the larger the exponent. Thus, Ångström exponent is a useful quantity to assess the particle size of atmospheric aerosols or clouds, and the wavelength dependence of the aerosol/cloud optical properties. For example, cloud droplet, usually with large sizes and thus very smaller Ångström exponent (nearly zero), is spectrally neutral, which means, e.g., the optical depth does not change with wavelength. This exponent is now routinely estimated by analyzing radiation measurements acquired on Earth Observation platforms, such as AErosol RObotic NETwork, or AERONET.

References

IPCC Third Assessment Report, has extensive coverage of aerosol-climate interactions.
Kuo-nan Liou (2002) An Introduction to Atmospheric Radiation, International Geophysics Series, No. 84, Academic Press, 583 p, ISBN 0-12-451451-0.

External links

This article is issued from Wikipedia - version of the 3/22/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Angstrom exponent

See also

References

External links