Amenable Banach algebra
A Banach algebra, A, is amenable if all bounded derivations from A into dual Banach A-bimodules are inner (that is of the form 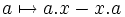 for some
for some 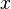 in the dual module).
in the dual module).
An equivalent characterization is that A is amenable if and only if it has a virtual diagonal.
Examples
- If A is a group algebra
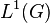 for some locally compact group G then A is amenable if and only if G is amenable.
for some locally compact group G then A is amenable if and only if G is amenable. - If A is a C*-algebra then A is amenable if and only if it is nuclear.
- If A is a uniform algebra on a compact Hausdorff space then A is amenable if and only if it is trivial (i.e. the algebra C(X) of all continuous complex functions on X).
- If A is amenable and there is a continuous algebra homomorphism
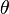 from A to another Banach algebra, then the closure of
from A to another Banach algebra, then the closure of 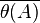 is amenable.
is amenable.
References
- F.F. Bonsall, J. Duncan, "Complete normed algebras", Springer-Verlag (1973).
- H.G. Dales, "Banach algebras and automatic continuity", Oxford University Press (2001).
- B.E. Johnson, "Cohomology in Banach algebras", Memoirs of the AMS 127 (1972).
- J.-P. Pier, "Amenable Banach algebras", Longman Scientific and Technical (1988).
This article is issued from Wikipedia - version of the 7/27/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.